题目内容
20. 如图,下列选项中能使平行四边形ABCD是菱形的条件有( )
如图,下列选项中能使平行四边形ABCD是菱形的条件有( )①AC⊥BD ②BA⊥AD ③AB=BC ④AC=BD.
| A. | ①③ | B. | ②③ | C. | ③④ | D. | ①②③ |
分析 四边形ABCD是平行四边形,要是其成为菱形,加上一组邻边相等或对角线垂直均可.
解答 解:因为一组邻边相等的平行四边形是菱形;对角线互相垂直平分的四边形是菱形.则能使?ABCD是菱形的有①或③.
故选:A.
点评 此题考查了菱形的判定,即对角线互相垂直的平行四边形是菱形,有一组邻边相等的平行四边形是菱形,需熟练掌握菱形的两个基本判定.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
11.将方程x2+8x+9=0配方后,原方程可变形为( )
| A. | (x+4)2=7 | B. | (x+4)2=25 | C. | (x+4)2=-9 | D. | (x+8)2=7 |
12.某工人若每小时生产38个零件,在规定时间内还有15个不能完成,若每小时生产42个零件,则可以超额完成5个,问:规定时间是多少?设规定时间为x小时,则可列方程为( )
| A. | 38x-15=42x+5 | B. | 38x+15=42x-5 | C. | 42x+38x=15+5 | D. | 42x-38x=15-5 |
9.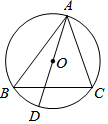 如图,⊙O是△ABC的外接圆,AD是⊙O的直径,若⊙O的半径为5,AC=8.则cosB的值是( )
如图,⊙O是△ABC的外接圆,AD是⊙O的直径,若⊙O的半径为5,AC=8.则cosB的值是( )
 如图,⊙O是△ABC的外接圆,AD是⊙O的直径,若⊙O的半径为5,AC=8.则cosB的值是( )
如图,⊙O是△ABC的外接圆,AD是⊙O的直径,若⊙O的半径为5,AC=8.则cosB的值是( )| A. | $\frac{4}{3}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{5}$ |
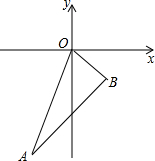 如图,直线OA的解析式为y=3x,点 A的横坐标是-1,OB=$\sqrt{2}$,OB与x轴所夹锐角是45°.
如图,直线OA的解析式为y=3x,点 A的横坐标是-1,OB=$\sqrt{2}$,OB与x轴所夹锐角是45°.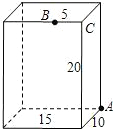 如图,长方体的长为15cm,宽为10cm,高为20cm,点B距离C点5cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,徐亚爬行的最短距离是25cm.
如图,长方体的长为15cm,宽为10cm,高为20cm,点B距离C点5cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,徐亚爬行的最短距离是25cm.