题目内容
19.用配方法解方程x2-4x-5=0时,原方程应变形为( )| A. | (x-2)2=9 | B. | (x-1)2=6 | C. | (x+1)2=6 | D. | (x+2)2=6 |
分析 先将常数项-5移到方程的右边,两边同时加上一次项系数一半的平方,即加4,左边为(x-2)2,右边化简,得结论.
解答 解:x2-4x-5=0,
x2-4x=5,
x2-4x+4=5+4,
(x-2)2=9,
故选A.
点评 本题考查了利用配方法解一元二次方程,熟练掌握配方法的步骤是关键:
①把原方程化为ax2+bx+c=0(a≠0)的形式;②方程两边同除以二次项系数,使二次项系数为1,并把常数项移到方程右边;③方程两边同时加上一次项系数一半的平方;④把左边配成一个完全平方式,右边化为一个常数;⑤如果右边是非负数,就可以进一步通过直接开平方法来求出它的解,如果右边是一个负数,则判定此方程无实数解.

练习册系列答案
相关题目
4.关于一次函数y=-2x+b(b为常数),下列说法正确的是( )
| A. | y随x的增大而增大 | |
| B. | 当b=4时,直线与坐标轴围成的面积是4 | |
| C. | 图象一定过第一、三象限 | |
| D. | 与直线y=3-2x相交于第四象限内一点 |
11.将方程x2+8x+9=0配方后,原方程可变形为( )
| A. | (x+4)2=7 | B. | (x+4)2=25 | C. | (x+4)2=-9 | D. | (x+8)2=7 |
9.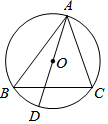 如图,⊙O是△ABC的外接圆,AD是⊙O的直径,若⊙O的半径为5,AC=8.则cosB的值是( )
如图,⊙O是△ABC的外接圆,AD是⊙O的直径,若⊙O的半径为5,AC=8.则cosB的值是( )
 如图,⊙O是△ABC的外接圆,AD是⊙O的直径,若⊙O的半径为5,AC=8.则cosB的值是( )
如图,⊙O是△ABC的外接圆,AD是⊙O的直径,若⊙O的半径为5,AC=8.则cosB的值是( )| A. | $\frac{4}{3}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{5}$ |
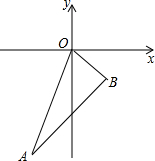 如图,直线OA的解析式为y=3x,点 A的横坐标是-1,OB=$\sqrt{2}$,OB与x轴所夹锐角是45°.
如图,直线OA的解析式为y=3x,点 A的横坐标是-1,OB=$\sqrt{2}$,OB与x轴所夹锐角是45°.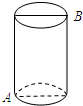 如图,圆柱体的高为12cm,底面周长为10cm,圆柱下底面A点除有一只蜘蛛,它想吃到上底面上与A点相对的B点处的苍蝇,需要爬行的最短路径是13cm.
如图,圆柱体的高为12cm,底面周长为10cm,圆柱下底面A点除有一只蜘蛛,它想吃到上底面上与A点相对的B点处的苍蝇,需要爬行的最短路径是13cm.