题目内容
18. 在数学课上,老师请同学思考如下问题:
在数学课上,老师请同学思考如下问题:已知:在△ABC中,∠A=90°.
求作:⊙P,使得点P在AC上,且⊙P与AB,BC都相切.
小轩的作法如下:
(1)作∠ABC的平分线BF,与AC交于点P;
(2)以点P为圆心,AP长为半径作⊙P.⊙P即为所求.
老师说:“小轩的作法正确.”
请回答:⊙P与BC相切的依据是角平分线上的点到角两边距离相等;经过半径的外端并且垂直于这条半径的直线是圆的切线(或:如果圆心到直线的距离等于半径,那么直线与圆相切).
分析 根据角平分线的性质定理以及圆的切线的两个判定定理即可解决问题.
解答 解:如图作PE⊥BC于E.
∵∠PBA=∠PBE,PA⊥AB,PE⊥BC,
∴PA=PE,
∴PE是⊙P的切线(角平分线上的点到角两边距离相等;经过半径的外端并且垂直于这条半径的直线是圆的切线.或:如果圆心到直线的距离等于半径,那么直线与圆相切)
故答案为角平分线上的点到角两边距离相等;经过半径的外端并且垂直于这条半径的直线是圆的切线(或:如果圆心到直线的距离等于半径,那么直线与圆相切).
点评 本题考查作图-复杂作图、切线的判定等知识,解题的关键是熟练掌握切线的两种判定方法,属于中考常考题型.

练习册系列答案
 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案
相关题目
9.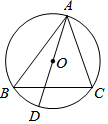 如图,⊙O是△ABC的外接圆,AD是⊙O的直径,若⊙O的半径为5,AC=8.则cosB的值是( )
如图,⊙O是△ABC的外接圆,AD是⊙O的直径,若⊙O的半径为5,AC=8.则cosB的值是( )
 如图,⊙O是△ABC的外接圆,AD是⊙O的直径,若⊙O的半径为5,AC=8.则cosB的值是( )
如图,⊙O是△ABC的外接圆,AD是⊙O的直径,若⊙O的半径为5,AC=8.则cosB的值是( )| A. | $\frac{4}{3}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{5}$ |
13.-$\frac{1}{2}$的相反数是( )
| A. | 2 | B. | -2 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
5.三角形三条边大小之间存在一定的关系,以下列各组线段为边,能组成三角形的是( )
| A. | 2cm、3cm、5cm | B. | 5cm、6cm、10cm | C. | 1cm、1cm、3cm | D. | 3cm、4cm、9cm |
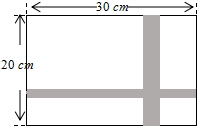 如图,要设计一副宽20cm、长30cm的图案,其中有一横一竖的彩条,横、竖彩条的宽度之比为2:3.如果要彩条所占面积是图案面积的19%,问横、竖彩条的宽度各为多少cm?
如图,要设计一副宽20cm、长30cm的图案,其中有一横一竖的彩条,横、竖彩条的宽度之比为2:3.如果要彩条所占面积是图案面积的19%,问横、竖彩条的宽度各为多少cm?