题目内容
1.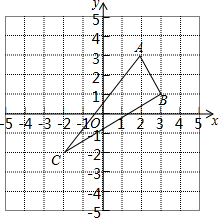 △ABC在平面直角坐标系中的位置如图所示.A(2,3),B(3,1),C(-2,-2)三点在格点上.
△ABC在平面直角坐标系中的位置如图所示.A(2,3),B(3,1),C(-2,-2)三点在格点上.(1)作出△ABC关于y轴对称的△A1B1C1;
(2)直接写出△ABC关于x轴对称的△A2B2C2的各点坐标;
(3)求出△ABC的面积.
分析 (1)先得到△ABC关于y轴对称的对应点,再顺次连接即可;
(2)先得到△ABC关于x轴对称的对应点,再顺次连接,并且写出△ABC关于x轴对称的△A2B2C2的各点坐标即可;
(3)利用轴对称图形的性质可得利用矩形的面积减去三个顶点上三角形的面积即可.
解答  解:(1)如图所示:
解:(1)如图所示:
(2)如图所示:A2(2,-3),B2(3,-1),C2(-2,2).
(3)S△ABC=5×5-$\frac{1}{2}$×3×5-$\frac{1}{2}$×1×2-$\frac{1}{2}$×5×4
=25-7.5-1-10
=6.5.
点评 本题考查的是作图-轴对称变换,熟知轴对称的性质是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.将方程x2+8x+9=0配方后,原方程可变形为( )
| A. | (x+4)2=7 | B. | (x+4)2=25 | C. | (x+4)2=-9 | D. | (x+8)2=7 |
12.某工人若每小时生产38个零件,在规定时间内还有15个不能完成,若每小时生产42个零件,则可以超额完成5个,问:规定时间是多少?设规定时间为x小时,则可列方程为( )
| A. | 38x-15=42x+5 | B. | 38x+15=42x-5 | C. | 42x+38x=15+5 | D. | 42x-38x=15-5 |
9.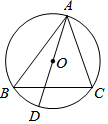 如图,⊙O是△ABC的外接圆,AD是⊙O的直径,若⊙O的半径为5,AC=8.则cosB的值是( )
如图,⊙O是△ABC的外接圆,AD是⊙O的直径,若⊙O的半径为5,AC=8.则cosB的值是( )
 如图,⊙O是△ABC的外接圆,AD是⊙O的直径,若⊙O的半径为5,AC=8.则cosB的值是( )
如图,⊙O是△ABC的外接圆,AD是⊙O的直径,若⊙O的半径为5,AC=8.则cosB的值是( )| A. | $\frac{4}{3}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{5}$ |
13.-$\frac{1}{2}$的相反数是( )
| A. | 2 | B. | -2 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
8.某天同时同地,甲同学测得1m的测竿在地面上影长为0.8m,乙同学测得国旗旗杆在地面上的影长为9.6m,则国旗旗杆的长为( )
| A. | 10m | B. | 12m | C. | 13m | D. | 15m |

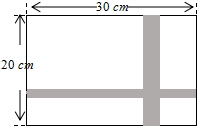 如图,要设计一副宽20cm、长30cm的图案,其中有一横一竖的彩条,横、竖彩条的宽度之比为2:3.如果要彩条所占面积是图案面积的19%,问横、竖彩条的宽度各为多少cm?
如图,要设计一副宽20cm、长30cm的图案,其中有一横一竖的彩条,横、竖彩条的宽度之比为2:3.如果要彩条所占面积是图案面积的19%,问横、竖彩条的宽度各为多少cm?