题目内容
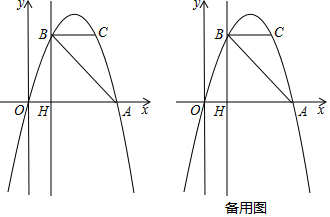
14. 如图,△ABC中,∠B=15°,∠ACB=25°,AB=4cm,△ABC逆时针旋转一定角度后与△ADE重合,且点C恰好成为AD的中点.
如图,△ABC中,∠B=15°,∠ACB=25°,AB=4cm,△ABC逆时针旋转一定角度后与△ADE重合,且点C恰好成为AD的中点.(1)指出旋转中心,并求出旋转的度数;
(2)求出∠BAE的度数和AE的长.
分析 (1)先利用三角形内角和计算出∠BAC=140°,然后根据旋转的定义求解;
(2)根据旋转的性质得∠EAD=∠BAC=140°,AE=AC,AD=AB=4,则可利用周角定义可计算出∠BAE=80°,然后计算出AC,从而得到AE的长.
解答 解:(1)∠BAC=180°-∠B-∠ACB=180°-15°-25°=140°,
即∠BAD=140°,
所以旋转中心为点A,旋转的度数为360°-140°=210°;
(2)∵△ABC逆时针旋转一定角度后与△ADE重合,
∴∠EAD=∠BAC=140°,AE=AC,AD=AB=4
∴∠BAE=360°-140°-140°=80°,
∵点C恰好成为AD的中点,
∴AC=$\frac{1}{2}$AD=2,
∴AE=2.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.

练习册系列答案
相关题目
2.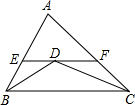 如图,△ABC中,BD,CD分别平分∠ABC,∠ACB,过点D作EF∥BC交AB,AC于点E,F,当∠A的位置及大小变化时,线段EF和BE+CF的大小关系为( )
如图,△ABC中,BD,CD分别平分∠ABC,∠ACB,过点D作EF∥BC交AB,AC于点E,F,当∠A的位置及大小变化时,线段EF和BE+CF的大小关系为( )
 如图,△ABC中,BD,CD分别平分∠ABC,∠ACB,过点D作EF∥BC交AB,AC于点E,F,当∠A的位置及大小变化时,线段EF和BE+CF的大小关系为( )
如图,△ABC中,BD,CD分别平分∠ABC,∠ACB,过点D作EF∥BC交AB,AC于点E,F,当∠A的位置及大小变化时,线段EF和BE+CF的大小关系为( )| A. | EF>BE+CF | B. | EF=BE+CF | C. | EF<BE+CF | D. | 不能确定 |
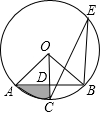 如图,点A、B、E在⊙O上,半径OC⊥AB于点D,∠CEB=22.5°,OD=$\sqrt{2}$,则图中阴影部分的面积等于$\frac{1}{2}π$-1.(结果保留π)
如图,点A、B、E在⊙O上,半径OC⊥AB于点D,∠CEB=22.5°,OD=$\sqrt{2}$,则图中阴影部分的面积等于$\frac{1}{2}π$-1.(结果保留π)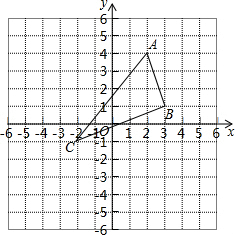 如图,在平面直角坐标系中,A(2,4),B(3,1),C(-2,-1).
如图,在平面直角坐标系中,A(2,4),B(3,1),C(-2,-1).