题目内容
6.如图,抛物线y=ax2+bx过A(4,0),B(1,3)两点,点C,B关于抛物线的对称轴对称,过点B作直线BH⊥x轴,交x轴于点H.(1)求抛物线的表达式;
(2)直接写出点C的坐标,并求出△ABC的面积;
(3)点P是抛物线上一动点,且位于第四象限,当△ABP的面积为6时,求出点P的坐标;
(4)若点M在直线BH上运动,点N在x轴上运动,当CM=MN,且∠CMN=90°时,求此时△CMN的面积.
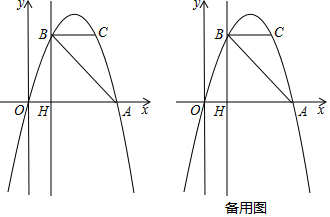
分析 (1)把点A(4,0),B(1,3)代入抛物线y=ax2+bx中,求得a、b的值,从而得到抛物线的解析式;
(2)先求得抛物线对称轴为x=2,由点B的坐标可得到点C的坐标,从而得到BC的长,然后依据三角形的面积公式求解即可
(3)过P点作PD⊥BH交BH于点D.设点P(m,-m2+4m),则BH=AH=3,HD=m2-4m,PD=m-1,然后依据S△ABP=S△ABH+S四边形HAPD-S△BPD,列出关于m的方程,从而可求得m的值于是可求得点P的坐标;
(4)①当点M在x轴上方时,先证明三角形△CBM≌△MHN,从而可求得BC=MH=2,BM=1,于是可得到点M,N的坐标,然后依据勾股定理求得MC的长,最后依据三角形的面积公式求解即可;②如图3所示:当点M在x轴下方时,过点M作平行与x轴的直线,然后分别过点N和点C作x轴的垂线,从而可构造出直角三角形Rt△NEM和Rt△MDC,接下来,再证明Rt△NEM≌Rt△MDC,依据全等三角形的性质可得到EM=CD=5,MD=ME=2,然后依据勾股定理可求得CM的长,最后依据三角形的面积公式求解即可.
解答 解:(1)把点A(4,0),B(1,3)代入抛物线y=ax2+bx中,得$\left\{\begin{array}{l}0=16a+4b\\ 3=a+b\end{array}\right.$解得:$\left\{\begin{array}{l}a=-1\\ b=4\end{array}\right.$,
∴抛物线表达式为:y=-x2+4x.
(2)抛物线对称轴为x=-$\frac{b}{2a}$=2.
∵点C,B关于抛物线的对称轴对称,点B的坐标为(1,3),
∴点C的坐标为(3,3).
∴BC=2,
∴S△ABC=$\frac{1}{2}$×2×3=3.
(3)过P点作PD⊥BH交BH于点D.
设点P(m,-m2+4m),
根据题意得:BH=AH=3,HD=m2-4m,PD=m-1,
∴S△ABP=S△ABH+S四边形HAPD-S△BPD,即6=$\frac{1}{2}$×3×3+$\frac{1}{2}$(3+m-1)(m2-4m)-$\frac{1}{2}$(m-1)(3+m2-4m).
整理得:3m2-15m=0,
解得:m1=0(舍去),m2=5,
∴点P坐标为(5,-5).
(4)当CM=MN,且∠CMN=90°时,分情况讨论:
①当点M在x轴上方时,如图2所示:
∵∠CMN=90°,
∴∠BMC+∠NMH=90°.
又∵∠BMC+∠BCM=90°,
∴∠NMH=∠BCM.
在△BCM和△HMN中$\left\{\begin{array}{l}{∠NMH=∠BCM}\\{∠CBM=∠MHN}\\{MC=MN}\end{array}\right.$,
∴△CBM≌△MHN.
∴BC=MH=2,BM=HN=3-2=1,
∴M(1,2),N(2,0),
由勾股定理得:MC=$\sqrt{{2^2}+{1^2}}$=$\sqrt{5}$,
∴S△CMN=$\frac{1}{2}$×$\sqrt{5}$×$\sqrt{5}$=$\frac{5}{2}$.
②当点M在x轴下方时,如图3所示:构造直角三角形Rt△NEM和Rt△MDC
∵∠NMC=90°,
∴∠NME+∠CMD=90°.
∵∠ENM+∠EMN=90°,
∴∠CMD=∠ENM.
在Rt△NEM和Rt△MDC中$\left\{\begin{array}{l}{∠CMD=∠ENM}\\{∠NEM=∠MDC}\\{MN=MC}\end{array}\right.$
∴Rt△NEM≌Rt△MDC.
∴EM=CD=5,MD=ME=2,
由勾股定理得:CM=$\sqrt{{2^2}+{5^2}}$=$\sqrt{29}$,
∴S△CMN=$\frac{1}{2}$×$\sqrt{29}$×$\sqrt{29}$=$\frac{29}{2}$;
综上所述:△CMN的面积为:$\frac{5}{2}$或$\frac{29}{2}$.
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求二次函数的解析式,全等三角形的性质和判定,作辅助线,构造出全的三角形,求得等腰直角三角形的直角边长是解题的关键.

 如图,在Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于点D.若BC=4cm,CD=3cm,则点D到AB的距离是( )
如图,在Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于点D.若BC=4cm,CD=3cm,则点D到AB的距离是( )| A. | 2cm | B. | 3cm | C. | 4cm | D. | 5cm |
 如图,△ABC≌△AED,AC与AD是对应边,AB与AE是对应边,则∠EAC等于( )
如图,△ABC≌△AED,AC与AD是对应边,AB与AE是对应边,则∠EAC等于( )| A. | ∠ACB | B. | ∠BAC | C. | ∠BAD | D. | ∠CAD |
 如图,矩形ABCD的对角线AC,BD相交于点O,以下说法不一定正确的是( )
如图,矩形ABCD的对角线AC,BD相交于点O,以下说法不一定正确的是( )| A. | ∠ABC=90° | B. | AC=BD | C. | ∠OAB=∠OBA | D. | OA=AD |
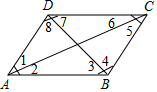 如图,若AB∥CD,则图中相等的内错角是( )
如图,若AB∥CD,则图中相等的内错角是( )| A. | ∠1与∠5,∠2与∠6 | B. | ∠3与∠7,∠4与∠8 | C. | ∠2与∠6,∠3与∠7 | D. | ∠1与∠5,∠4与∠8 |
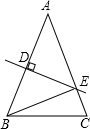 如图所示,在△ABC中,AB=AC,DE是AB的垂直平分线,△BCE的周长为14cm,BC=6cm,则AB=8cm.
如图所示,在△ABC中,AB=AC,DE是AB的垂直平分线,△BCE的周长为14cm,BC=6cm,则AB=8cm. 如图,△ABC中,∠B=15°,∠ACB=25°,AB=4cm,△ABC逆时针旋转一定角度后与△ADE重合,且点C恰好成为AD的中点.
如图,△ABC中,∠B=15°,∠ACB=25°,AB=4cm,△ABC逆时针旋转一定角度后与△ADE重合,且点C恰好成为AD的中点. 如图,在平面直角坐标系中,⊙M与x轴相切于点A(8,0),与y轴分别交于点B(0,4)和点C(0,16),则圆心M的坐标为(8,10).
如图,在平面直角坐标系中,⊙M与x轴相切于点A(8,0),与y轴分别交于点B(0,4)和点C(0,16),则圆心M的坐标为(8,10).