题目内容
4.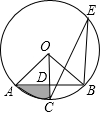 如图,点A、B、E在⊙O上,半径OC⊥AB于点D,∠CEB=22.5°,OD=$\sqrt{2}$,则图中阴影部分的面积等于$\frac{1}{2}π$-1.(结果保留π)
如图,点A、B、E在⊙O上,半径OC⊥AB于点D,∠CEB=22.5°,OD=$\sqrt{2}$,则图中阴影部分的面积等于$\frac{1}{2}π$-1.(结果保留π)
分析 由垂径定理得到$\widehat{AC}$=$\widehat{BC}$,根据圆周角定理得到∠AOC=2∠E=45°,推出△AOD是等腰直角三角形,由等腰三角形的性质得到AD=OD=$\sqrt{2}$,根据勾股定理得到OA=$\sqrt{2}$OD=2,根据扇形和三角形的面积公式即可得到结论.
解答 解:∵半径OC⊥AB于点D,
∴$\widehat{AC}$=$\widehat{BC}$,
∴∠AOC=2∠E=45°,
∴△AOD是等腰直角三角形,
∴AD=OD=$\sqrt{2}$,
∴OA=$\sqrt{2}$OD=2,
∴阴影部分的面积=S扇形AOC-S△AOD=$\frac{45•π×{2}^{2}}{360}$-$\frac{1}{2}×$$\sqrt{2}$×$\sqrt{2}$=$\frac{1}{2}π$-1.
故答案为:$\frac{1}{2}π$-1.
点评 本题考查了圆周角定理,垂径定理,扇形面积的计算,正确的识别图形是解题的关键.

练习册系列答案
相关题目
19. 如图,在正方形网格中有四个三角形,其中与△ABC相似(不包括△ABC本身)的三角形有( )
如图,在正方形网格中有四个三角形,其中与△ABC相似(不包括△ABC本身)的三角形有( )
 如图,在正方形网格中有四个三角形,其中与△ABC相似(不包括△ABC本身)的三角形有( )
如图,在正方形网格中有四个三角形,其中与△ABC相似(不包括△ABC本身)的三角形有( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
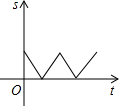
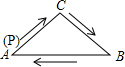 如图,在△ABC中,AC=BC,有一动点P从A出发,沿A→C→B→A匀速运动.设点P的运动时间为t,CP的长度s,则s与t之间的函数关系用图象描述大致是( )
如图,在△ABC中,AC=BC,有一动点P从A出发,沿A→C→B→A匀速运动.设点P的运动时间为t,CP的长度s,则s与t之间的函数关系用图象描述大致是( )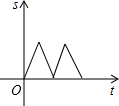
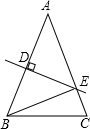 如图所示,在△ABC中,AB=AC,DE是AB的垂直平分线,△BCE的周长为14cm,BC=6cm,则AB=8cm.
如图所示,在△ABC中,AB=AC,DE是AB的垂直平分线,△BCE的周长为14cm,BC=6cm,则AB=8cm. 如图,△ABC中,∠B=15°,∠ACB=25°,AB=4cm,△ABC逆时针旋转一定角度后与△ADE重合,且点C恰好成为AD的中点.
如图,△ABC中,∠B=15°,∠ACB=25°,AB=4cm,△ABC逆时针旋转一定角度后与△ADE重合,且点C恰好成为AD的中点.