题目内容
20.已知D是△ABC的边BC所在直线上的一点,与B,C不重合,过D分别作DF∥AC交AB所在直接于F,DE∥AB交AC所在直线于E.若∠A=80°,则∠FDE的度数是80°或100°..分析 分为三种情况,画出图形,根据三角形的内角和定理求出∠BAC,再根据平行线的性质求出∠E,即可求出答案.
解答  解:分为三种情况:
解:分为三种情况:
第一种情况:如图①,∵∠A=80°,
∵DE∥AB,DF∥AC,
∴∠A=∠DFB,∠FDE=∠DFB,
∴∠FDE=∠A=80°;
第二种情况:如图②,∵∠BAC=80°,
∵DE∥AB,DF∥AC,
∴∠BAC=∠E=80°,∠FDE+∠E=180°,
∴∠FDE=100°;
第三种情况:如图③,∵∠BAC=80°,
∵DE∥AB,DF∥AC,
∴∠BAC=∠E=80°,∠FDE+∠E=180°,
∴∠FDE=100°;
故答案为:80°或100°.
点评 本题考查了平行线的性质和三角形内角和定理的应用,能求出符合条件的所有情况是解此题的关键,用了分类讨论思想.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
8.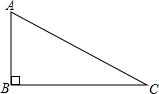 如图,△ABC中,∠B=90°,AB=3,BC=4,则cosA等于( )
如图,△ABC中,∠B=90°,AB=3,BC=4,则cosA等于( )
 如图,△ABC中,∠B=90°,AB=3,BC=4,则cosA等于( )
如图,△ABC中,∠B=90°,AB=3,BC=4,则cosA等于( )| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{4}{5}$ | D. | $\frac{3}{5}$ |
12. 如图,在平面直角坐标系中,直线y=-$\frac{3}{2}x+3$与矩形OABC的边AB、BC分别交于点E、F,若点B的坐标为(m,2),则m的值可能为( )
如图,在平面直角坐标系中,直线y=-$\frac{3}{2}x+3$与矩形OABC的边AB、BC分别交于点E、F,若点B的坐标为(m,2),则m的值可能为( )
 如图,在平面直角坐标系中,直线y=-$\frac{3}{2}x+3$与矩形OABC的边AB、BC分别交于点E、F,若点B的坐标为(m,2),则m的值可能为( )
如图,在平面直角坐标系中,直线y=-$\frac{3}{2}x+3$与矩形OABC的边AB、BC分别交于点E、F,若点B的坐标为(m,2),则m的值可能为( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{5}{2}$ | D. | $\frac{7}{2}$ |
9.下列运算中,正确的是( )
| A. | x•x3=x3 | B. | (x2)3=x5 | C. | x6÷x2=x4 | D. | (x-y)2=x2+y2 |
 如图,正方形ABCD中,AB=2,点E为BC边上的一个动点,连接AE,作∠EAF=45°,交CD边于点F,连接EF.若设BE=x,则△CEF的周长为4.
如图,正方形ABCD中,AB=2,点E为BC边上的一个动点,连接AE,作∠EAF=45°,交CD边于点F,连接EF.若设BE=x,则△CEF的周长为4.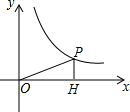 如图,P(12,a)在反比例函数$y=\frac{60}{x}$图象上,PH⊥x轴于H,则tan∠POH的值为$\frac{5}{12}$.
如图,P(12,a)在反比例函数$y=\frac{60}{x}$图象上,PH⊥x轴于H,则tan∠POH的值为$\frac{5}{12}$. 甲、乙两地相距400千米,一辆货车和一辆轿车先后从甲地出发向乙地,如图,线段OA(l货)表示货车离甲地距离y(千米)与货车出发时间x(小时)之间的函数关系;折线BCD表示轿车离甲地距离y(千米)与货车出发时间x(小时)之间的函数关系,请根据图象解答下列问题:
甲、乙两地相距400千米,一辆货车和一辆轿车先后从甲地出发向乙地,如图,线段OA(l货)表示货车离甲地距离y(千米)与货车出发时间x(小时)之间的函数关系;折线BCD表示轿车离甲地距离y(千米)与货车出发时间x(小时)之间的函数关系,请根据图象解答下列问题: