题目内容
18.若反比例函数y=$\frac{k}{x}$的图象位于第二、四象限,则k的取值可能是( )| A. | -1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据反比例函数的性质可知“当k<0时,函数图象位于第二、四象限”,结合四个选项即可得出结论.
解答 解:∵反比例函数y=$\frac{k}{x}$的图象位于第二、四象限,
∴k<0.
结合4个选项可知k=-1.
故选A.
点评 本题考查了反比例函数的性质,解题的关键是找出k<0.本题属于基础题,难度不大,解决该题型题目时,结合函数图象所在的象限找出k值的取值范围是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.已知反比例函数y=-$\frac{3}{x}$,下列结论不正确的是( )
| A. | 图象必经过点(-1,3) | B. | 两个分支分布在第二、四象限 | ||
| C. | 若x>1,则-3<y<0 | D. | y随x的增大而增大 |
3.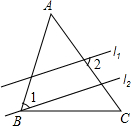 如图,直线l1∥l2,且分别与△ABC的两边AB、AC相交,若∠A=50°,∠1=55°,则∠2的大小为( )
如图,直线l1∥l2,且分别与△ABC的两边AB、AC相交,若∠A=50°,∠1=55°,则∠2的大小为( )
 如图,直线l1∥l2,且分别与△ABC的两边AB、AC相交,若∠A=50°,∠1=55°,则∠2的大小为( )
如图,直线l1∥l2,且分别与△ABC的两边AB、AC相交,若∠A=50°,∠1=55°,则∠2的大小为( )| A. | 55° | B. | 65° | C. | 75° | D. | 85° |
7.在△ABC中,∠A=90°,AB=3,BC=5,则sinB的值是( )
| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{3}{5}$ |
8.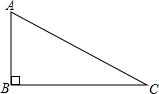 如图,△ABC中,∠B=90°,AB=3,BC=4,则cosA等于( )
如图,△ABC中,∠B=90°,AB=3,BC=4,则cosA等于( )
 如图,△ABC中,∠B=90°,AB=3,BC=4,则cosA等于( )
如图,△ABC中,∠B=90°,AB=3,BC=4,则cosA等于( )| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{4}{5}$ | D. | $\frac{3}{5}$ |
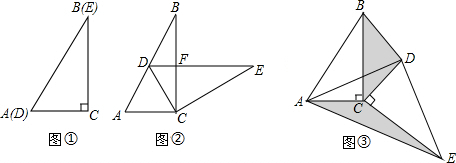
 如图,正方形ABCD中,AB=2,点E为BC边上的一个动点,连接AE,作∠EAF=45°,交CD边于点F,连接EF.若设BE=x,则△CEF的周长为4.
如图,正方形ABCD中,AB=2,点E为BC边上的一个动点,连接AE,作∠EAF=45°,交CD边于点F,连接EF.若设BE=x,则△CEF的周长为4.