题目内容
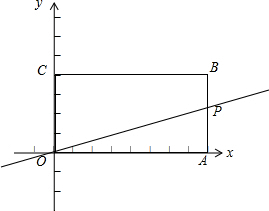 如图,长方形OABC边BC=4,AB=2.
如图,长方形OABC边BC=4,AB=2.(1)直线y=kx(k≠0),交边AB于点P,求k的取值范围;
(2)直线y=kx(k≠0),将长方形OABC的面积分成两部分,靠近y轴的一部分记作S,试写出S关于k的解析式;
(3)直线y=kx(k≠0),是否可能将长方形OABC的面积分成两部分的面积比为2:3?若能,求出k的值;若不能,说明理由.
考点:一次函数综合题
专题:
分析:(1)根据题意直线y=kx必须相交于线段AB即可求得k的取值范围;
(2)分三种情况分别讨论求得;
(3)直线y=kx(k≠0),将长方形OABC的面积分成两部分的面积比为2:3,有两种情况,一种是靠近y轴的一部分是
,另一种是靠近y轴的一部分是
,进而列出方程,解方程即可求得.
(2)分三种情况分别讨论求得;
(3)直线y=kx(k≠0),将长方形OABC的面积分成两部分的面积比为2:3,有两种情况,一种是靠近y轴的一部分是
| 2 |
| 5 |
| 3 |
| 5 |
解答:解:(1)∵直线y=kx(k≠0),交边AB于点P,
∴直线y=kx(k≠0)经过一、三象限,
∴k>0,
把B(4,2)代入y=kx(k≠0),得2=4k,
解得k=
,
∴直线y=kx(k≠0),交边AB于点P,求k的取值范围为0<k≤
;
(2)有三种情况:
①当直线y=kx交BC于P时,解
解得x=
,
∴P(
,2),
∴S=
×
×2=
,
即S=
(k>
);
②当直线y=kx经过B点时,
S=
×4×2=4,
③当直线y=kx交AB于P时,解
,解得y=4k,
∴S=S矩形-S△AOP=4×2-
×4×4k=8-8k,
即S=-8k+8(0<k<
);
综上所述,S关于k的解析式为:S=
;
(3)能;
∵S矩形=8,直线y=kx(k≠0)将长方形OABC的面积分成两部分的面积比为2:3,
当直线y=kx交BC于P时,S△POC=8×
=
,
∵S=
,
∴
=
,解得k=
;
当直线y=kx交AB于P时,S△AOP=
,
∵S△AOP=
×4×4k=8k,
∴8k=
,解得,k=
;
所以直线y=kx(k≠0),将长方形OABC的面积分成两部分的面积比为2:3时,k的值为
或
.
∴直线y=kx(k≠0)经过一、三象限,
∴k>0,
把B(4,2)代入y=kx(k≠0),得2=4k,
解得k=
| 1 |
| 2 |
∴直线y=kx(k≠0),交边AB于点P,求k的取值范围为0<k≤
| 1 |
| 2 |
(2)有三种情况:
①当直线y=kx交BC于P时,解
|
| 2 |
| k |
∴P(
| 2 |
| k |
∴S=
| 1 |
| 2 |
| 2 |
| k |
| 2 |
| k |
即S=
| 2 |
| k |
| 1 |
| 2 |
②当直线y=kx经过B点时,
S=
| 1 |
| 2 |
③当直线y=kx交AB于P时,解
|
∴S=S矩形-S△AOP=4×2-
| 1 |
| 2 |
即S=-8k+8(0<k<
| 1 |
| 2 |
综上所述,S关于k的解析式为:S=
|
(3)能;
∵S矩形=8,直线y=kx(k≠0)将长方形OABC的面积分成两部分的面积比为2:3,
当直线y=kx交BC于P时,S△POC=8×
| 2 |
| 5 |
| 16 |
| 5 |
∵S=
| 2 |
| k |
∴
| 2 |
| k |
| 16 |
| 5 |
| 5 |
| 8 |
当直线y=kx交AB于P时,S△AOP=
| 16 |
| 5 |
∵S△AOP=
| 1 |
| 2 |
∴8k=
| 16 |
| 5 |
| 2 |
| 5 |
所以直线y=kx(k≠0),将长方形OABC的面积分成两部分的面积比为2:3时,k的值为
| 2 |
| 5 |
| 5 |
| 8 |
点评:本题是一次函数的综合题,考查了直线上的点的特征,待定系数法求解析式,以及三角形的面积等,数形结合思想的运用是本题的关键.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
用较为简便的方法计算:
(1)(+5)-(-4)+(-7)-(+4)+(-3)
(2)(
-
+
)×36
(3)
-(-1
)+(-1
)-
(4)5.7-4.2-8.4-2.3+1
.
(1)(+5)-(-4)+(-7)-(+4)+(-3)
(2)(
| 3 |
| 4 |
| 7 |
| 9 |
| 1 |
| 6 |
(3)
| 2 |
| 9 |
| 5 |
| 6 |
| 2 |
| 9 |
| 1 |
| 3 |
(4)5.7-4.2-8.4-2.3+1
| 1 |
| 5 |
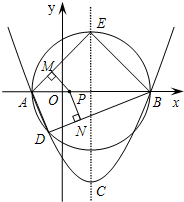 已知:抛物线y=ax2+bx+c(a≠0),顶点C(1,-3),与x轴交于A、B两点,A(-1,0).
已知:抛物线y=ax2+bx+c(a≠0),顶点C(1,-3),与x轴交于A、B两点,A(-1,0).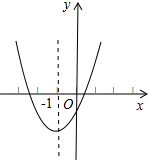 已知二次函数y=ax2+bx+c的图象如图,其对称轴x=-1,给出下列结果:
已知二次函数y=ax2+bx+c的图象如图,其对称轴x=-1,给出下列结果: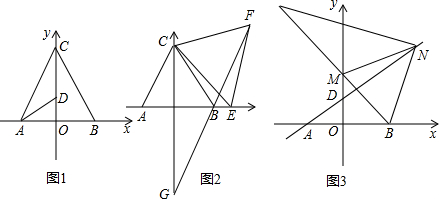
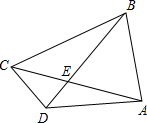 如图所示,已知四边形ABCD的对角线AC、BD相交于点E,△AED∽△BEC,其中A、E、D三点的对应点分别为B、E、C三点,∠ADE=∠ACD,若△ABE的面积为16,△CDE的面积为4,AD=7,DE:BE=1:3.
如图所示,已知四边形ABCD的对角线AC、BD相交于点E,△AED∽△BEC,其中A、E、D三点的对应点分别为B、E、C三点,∠ADE=∠ACD,若△ABE的面积为16,△CDE的面积为4,AD=7,DE:BE=1:3.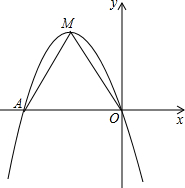 已知抛物线y=a(x+1)2+2经过原点,且与x轴相交于另外一点A,M是它的顶点.将△OAM绕点O逆时针旋转90°,得到△OA′M′.
已知抛物线y=a(x+1)2+2经过原点,且与x轴相交于另外一点A,M是它的顶点.将△OAM绕点O逆时针旋转90°,得到△OA′M′. 如图,过正方形ABCD的顶点作对角线BD的平行线,在这条线上取一点E,使BE=BD,连结DE,BE交AD于F,求证:DE2=EF•DB.
如图,过正方形ABCD的顶点作对角线BD的平行线,在这条线上取一点E,使BE=BD,连结DE,BE交AD于F,求证:DE2=EF•DB.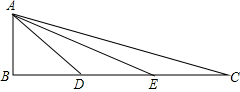 如图,在△ABC中,∠B=90°,点D、E在BC上,且AB=BD=EC=DE,求证:
如图,在△ABC中,∠B=90°,点D、E在BC上,且AB=BD=EC=DE,求证: