题目内容
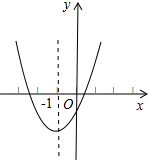 已知二次函数y=ax2+bx+c的图象如图,其对称轴x=-1,给出下列结果:
已知二次函数y=ax2+bx+c的图象如图,其对称轴x=-1,给出下列结果:①b2>4ac;②abc>0;③8a+c<0;④4a+2b+c>0;⑤a-b+c<0.
则正确的结论有( )个.
| A、2个 | B、3个 | C、4个 | D、5个 |
考点:二次函数图象与系数的关系
专题:
分析:根据抛物线与x轴的交点情况,抛物线的开口方向,对称轴及与y轴的交点,当x=2或x=-1时的函数值,逐一判断.
解答:解:①由图知:抛物线与x轴有两个不同的交点,则△=b2-4ac>0,b2>4ac,故①正确;
②抛物线开口向上,得:a>0;
抛物线的对称轴为x=-
=-1,b=2a,故b>0;
抛物线交y轴于负半轴,得:c<0;
所以abc<0;
故②错误;
③根据②可将抛物线的解析式化为:y=ax2+2ax+c(a≠0);
由函数的图象知:当x=2时,y>0;即4a+4a+c=8a+c>0,故③错误;
④当x=2时,y>0,即4a+2b+c>0,故④正确;
⑤当x=-1时,y<0,即a-b+c<0,故⑤正确;
故正确的结论有3个.
故选:B.
②抛物线开口向上,得:a>0;
抛物线的对称轴为x=-
| b |
| 2a |
抛物线交y轴于负半轴,得:c<0;
所以abc<0;
故②错误;
③根据②可将抛物线的解析式化为:y=ax2+2ax+c(a≠0);
由函数的图象知:当x=2时,y>0;即4a+4a+c=8a+c>0,故③错误;
④当x=2时,y>0,即4a+2b+c>0,故④正确;
⑤当x=-1时,y<0,即a-b+c<0,故⑤正确;
故正确的结论有3个.
故选:B.
点评:此题主要考查了图象与二次函数系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换,根的判别式的熟练运用.

练习册系列答案
相关题目
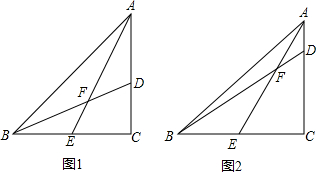 在△ABC中,AC=BC,∠ACB=90°,E是线段BC的中点,D在边AC上,线段BD和AE交于点F.
在△ABC中,AC=BC,∠ACB=90°,E是线段BC的中点,D在边AC上,线段BD和AE交于点F. 如图,已知△ABC中,AD,BF为BC,AC边上的高,过D作AB的垂线交AB于E,交BF于G,交AC的延长线于H,求证:DE2=EG•EH.
如图,已知△ABC中,AD,BF为BC,AC边上的高,过D作AB的垂线交AB于E,交BF于G,交AC的延长线于H,求证:DE2=EG•EH.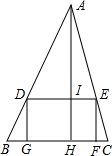 如图,在△ABC中,内接矩形DEFG,其中,点D、E分别在边AB、AC上,点G、F在边BC上,如果EF:DE=2:3,BC=8,高AH交DE于点I,且AH=10,求四边形DEFG的周长.
如图,在△ABC中,内接矩形DEFG,其中,点D、E分别在边AB、AC上,点G、F在边BC上,如果EF:DE=2:3,BC=8,高AH交DE于点I,且AH=10,求四边形DEFG的周长.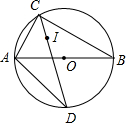 如图,AB是⊙O的直径,点C是⊙O上一点,点I是△ABC(AC<AB)的内心,CI的延长线交⊙O于点D,连AD.
如图,AB是⊙O的直径,点C是⊙O上一点,点I是△ABC(AC<AB)的内心,CI的延长线交⊙O于点D,连AD.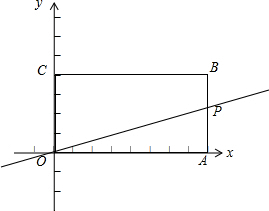 如图,长方形OABC边BC=4,AB=2.
如图,长方形OABC边BC=4,AB=2. 已知∠B=60°,∠C=40°,∠ADC=3∠A,求∠A.
已知∠B=60°,∠C=40°,∠ADC=3∠A,求∠A.