题目内容
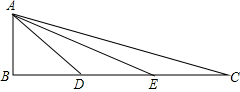 如图,在△ABC中,∠B=90°,点D、E在BC上,且AB=BD=EC=DE,求证:
如图,在△ABC中,∠B=90°,点D、E在BC上,且AB=BD=EC=DE,求证:(1)△ADE∽△CDA;
(2)∠C+∠AEB=45°.
考点:相似三角形的判定与性质
专题:常规题型
分析:(1)根据对应角相等、对应边比例相等可以求证;
(2)根据相似三角形对应角相等性质可以求解.
(2)根据相似三角形对应角相等性质可以求解.
解答:解:(1)∵∠B=90°,AB=BD,
∴AD=
AB,
∴
=
=
,
∵∠ADE=∠ADC
∴△ADE∽△CDA;
(2)∵△ADE∽△CDA
∴∠C=∠EAD,
∵∠EAD+∠AEB=45°,
∴∠C+∠AEB=45°.
∴AD=
| 2 |
∴
| DE |
| AD |
| AD |
| CD |
| ||
| 2 |
∵∠ADE=∠ADC
∴△ADE∽△CDA;
(2)∵△ADE∽△CDA
∴∠C=∠EAD,
∵∠EAD+∠AEB=45°,
∴∠C+∠AEB=45°.
点评:本题考查了相似三角形的判定,考查了相似三角形对应角相等的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列各点在抛物线y=-x2+1上的是( )
| A、(1,0) |
| B、(0,0) |
| C、(0,-1) |
| D、(1,1) |
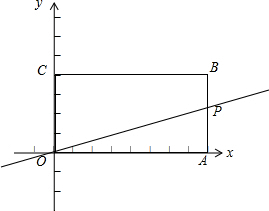 如图,长方形OABC边BC=4,AB=2.
如图,长方形OABC边BC=4,AB=2. 已知∠B=60°,∠C=40°,∠ADC=3∠A,求∠A.
已知∠B=60°,∠C=40°,∠ADC=3∠A,求∠A.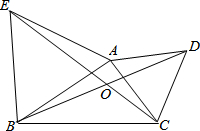 图中△ABE和△ACD都是等边三角形,BD与CE相交于点O.
图中△ABE和△ACD都是等边三角形,BD与CE相交于点O.