题目内容
 如图,过正方形ABCD的顶点作对角线BD的平行线,在这条线上取一点E,使BE=BD,连结DE,BE交AD于F,求证:DE2=EF•DB.
如图,过正方形ABCD的顶点作对角线BD的平行线,在这条线上取一点E,使BE=BD,连结DE,BE交AD于F,求证:DE2=EF•DB.考点:相似三角形的判定与性质,正方形的性质
专题:证明题
分析:作辅助线,构造直角三角形,求出∠DBE的度数,进而求出∠DFE的度数;证明△DEF∽△BED,问题即可解决.
解答: 证明:如图,连接AC,过点E作EP⊥BD于点P;
证明:如图,连接AC,过点E作EP⊥BD于点P;
∵四边形ABCD是正方形,
∴AC⊥BD,AO=
AC=
BD;
又∵AE∥BD,
∴四边形AEPO是矩形,
∴EP=AO=
BD,
又∵BE=BD,
∴EP=
BE,
∴∠EBP=30°;
∵BE=BD,
∴∠BED=∠BDE=
=75°,
∵∠DFE=45°+30°=75°,
∴∠DEF=∠DFE=∠BDE=75°,
∴△DEF∽△BED,
∴
=
,
∴DE2=EF•DB.
 证明:如图,连接AC,过点E作EP⊥BD于点P;
证明:如图,连接AC,过点E作EP⊥BD于点P;∵四边形ABCD是正方形,
∴AC⊥BD,AO=
| 1 |
| 2 |
| 1 |
| 2 |
又∵AE∥BD,
∴四边形AEPO是矩形,
∴EP=AO=
| 1 |
| 2 |
又∵BE=BD,
∴EP=
| 1 |
| 2 |
∴∠EBP=30°;
∵BE=BD,
∴∠BED=∠BDE=
| 180°-30° |
| 2 |
∵∠DFE=45°+30°=75°,
∴∠DEF=∠DFE=∠BDE=75°,
∴△DEF∽△BED,
∴
| DE |
| DB |
| EF |
| DE |
∴DE2=EF•DB.
点评:该命题以正方形为载体,在考查正方形性质定理的同时,重点考查了直角三角形的性质、三角形的内角和定理、相似三角形的判定及其应用等几何知识点;准确作出辅助线是解题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
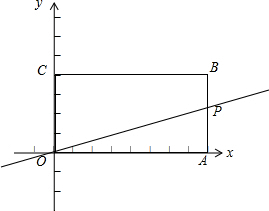 如图,长方形OABC边BC=4,AB=2.
如图,长方形OABC边BC=4,AB=2.
 已知∠B=60°,∠C=40°,∠ADC=3∠A,求∠A.
已知∠B=60°,∠C=40°,∠ADC=3∠A,求∠A.