题目内容
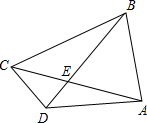如图所示，已知四边形ABCD的对角线AC、BD相交于点E，△AED∽△BEC，其中A、E、D三点的对应点分别为B、E、C三点，∠ADE=∠ACD，若△ABE的面积为16，△CDE的面积为4，AD=7，DE：BE=1：3．（1）求
| DE |
| AE |
（2）求AC的长．
考点：相似三角形的判定与性质
专题：常规题型
分析：（1）根据相似三角形面积比是对应边比例的平方即可解题；
（2）易证△DEA∽△CDA，即可求得AC的值．
（2）易证△DEA∽△CDA，即可求得AC的值．
解答：解：如图
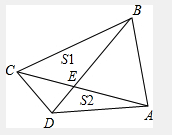
（1）记△BCE面积为S1，△AED面积为S2，
=
=
，
∴S1=12，
=
=
，
∴S2=
，
∵
=(
)2，
∴
=
，
设DE=a，则CE=
a，
∵
=
，
∴EA=2a，
∴
=
，
（2）∵∠EDA=∠DCA，∠EAD=∠CAD，
∴△DEA∽△CDA，
∴
=
，
∵AD=7，
∴49=2a+
a，
∵a＞0，
∴a=
，
∴AC=
．
（1）记△BCE面积为S1，△AED面积为S2，
| S1 |
| S△CDE |
| BE |
| DE |
| 3 |
| 1 |
∴S1=12，
| S2 |
| S△ABE |
| DE |
| BE |
| 1 |
| 3 |
∴S2=
| 16 |
| 3 |
∵
| S1 |
| S2 |
| CE |
| DE |
∴
| CE |
| DE |
| 1 |
| 3 |
设DE=a，则CE=
| 3 |
| 2 |
∵
| S△CDE |
| S2 |
| CE |
| EA |
∴EA=2a，
∴
| DE |
| AE |
| 1 |
| 2 |
（2）∵∠EDA=∠DCA，∠EAD=∠CAD，
∴△DEA∽△CDA，
∴
| AD |
| CA |
| AE |
| AD |
∵AD=7，
∴49=2a+
| 7 |
| 2 |
∵a＞0，
∴a=
| ||
| 2 |
∴AC=
7
| ||
| 4 |
点评：本题考查了相似三角形面积比是对应边比值的平方，考查了相似三角形的判定．
练习册系列答案
举一反三单元同步过关卷系列答案
相关题目
如图，已知△ABC中，AD，BF为BC，AC边上的高，过D作AB的垂线交AB于E，交BF于G，交AC的延长线于H，求证：DE2=EG•EH．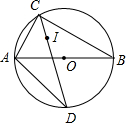
如图，AB是⊙O的直径，点C是⊙O上一点，点I是△ABC（AC＜AB）的内心，CI的延长线交⊙O于点D，连AD．
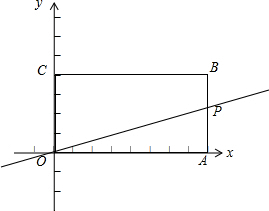如图，长方形OABC边BC=4，AB=2．
如图，在△ABC中，AB=8，AC=6，BC=10．线段BC所在直线以每秒2个单位的速度沿与其垂直的方向上平行移动，记x秒时，该直线在△ABC内的部分的长度为y．试写出y关于x的函数关系式，并在平面直角坐标系中画出这一函数的图象．
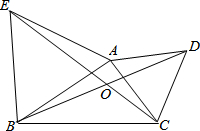图中△ABE和△ACD都是等边三角形，BD与CE相交于点O．