题目内容
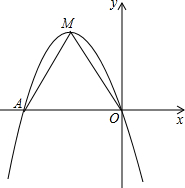 已知抛物线y=a(x+1)2+2经过原点,且与x轴相交于另外一点A,M是它的顶点.将△OAM绕点O逆时针旋转90°,得到△OA′M′.
已知抛物线y=a(x+1)2+2经过原点,且与x轴相交于另外一点A,M是它的顶点.将△OAM绕点O逆时针旋转90°,得到△OA′M′.(1)画出△OA′M′,并求a的值;
(2)求线段AM′的长度.
考点:二次函数的性质,作图-旋转变换
专题:
分析:(1)利用图形旋转的性质得出对应点位置进而得出答案,再利用图象过(0,0),进而得出答案;
(2)利用全等三角形的判定与性质得出△MNO≌△OAM′(SAS),进而得出答案.
(2)利用全等三角形的判定与性质得出△MNO≌△OAM′(SAS),进而得出答案.
解答: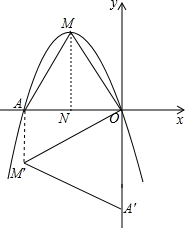 解:(1)如图所示:△OA′M′即为所求;
解:(1)如图所示:△OA′M′即为所求;
∵抛物线y=a(x+1)2+2经过原点,
∴0=a(0+1)2+2,
解得:a=-2;
(2)连接AM′,过点M作MN⊥AO于点N,
∵抛物线y=-2(x+1)2+2,
当y=0,则0=-2(x+1)2+2
解得:x1=0,x2=-2,
故AO=2,
∵M是抛物线的顶点,
∴MN=2,NO=1,
故MO=M′O=
,
∵∠NMO+∠MON=90°,∠MOA+∠AOM=90°,
∴∠OMN=∠AOM,
在△MNO和△OAM′中
∵
,
∴△MNO≌△OAM′(SAS),
∴AM′=NO=1.
 解:(1)如图所示:△OA′M′即为所求;
解:(1)如图所示:△OA′M′即为所求;∵抛物线y=a(x+1)2+2经过原点,
∴0=a(0+1)2+2,
解得:a=-2;
(2)连接AM′,过点M作MN⊥AO于点N,
∵抛物线y=-2(x+1)2+2,
当y=0,则0=-2(x+1)2+2
解得:x1=0,x2=-2,
故AO=2,
∵M是抛物线的顶点,
∴MN=2,NO=1,
故MO=M′O=
| 5 |
∵∠NMO+∠MON=90°,∠MOA+∠AOM=90°,
∴∠OMN=∠AOM,
在△MNO和△OAM′中
∵
|
∴△MNO≌△OAM′(SAS),
∴AM′=NO=1.
点评:此题主要考查了全等三角形的判定与性质以及旋转的性质,得出△MNO≌△OAM′是解题关键.

练习册系列答案
相关题目
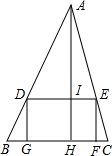 如图,在△ABC中,内接矩形DEFG,其中,点D、E分别在边AB、AC上,点G、F在边BC上,如果EF:DE=2:3,BC=8,高AH交DE于点I,且AH=10,求四边形DEFG的周长.
如图,在△ABC中,内接矩形DEFG,其中,点D、E分别在边AB、AC上,点G、F在边BC上,如果EF:DE=2:3,BC=8,高AH交DE于点I,且AH=10,求四边形DEFG的周长.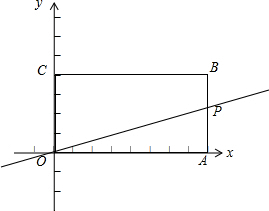 如图,长方形OABC边BC=4,AB=2.
如图,长方形OABC边BC=4,AB=2. 如图,△ABC中,DE∥BC,BE、CD相交于F,S△EFC=3S△DEF,求S△ADE:S△DBE:S△ABC.
如图,△ABC中,DE∥BC,BE、CD相交于F,S△EFC=3S△DEF,求S△ADE:S△DBE:S△ABC.