题目内容
17. 如图,Rt△OAB中,∠AOB=90°,OA=6,OB=8,P、Q分别是OB、OA上的动点,满足BP=OQ,C为PQ中点,当Q从O点运动到点A点时,则C点所走过的路径长为3$\sqrt{2}$.
如图,Rt△OAB中,∠AOB=90°,OA=6,OB=8,P、Q分别是OB、OA上的动点,满足BP=OQ,C为PQ中点,当Q从O点运动到点A点时,则C点所走过的路径长为3$\sqrt{2}$.
分析 如图,当点Q与O重合,点P与B重合,此时点C与OB的中点E重合,当点Q与A重合时,点P在点M处,BM=OA=6,此时点C在AM的中点F处,由此可知点C的运动轨迹是线段FE(红线),在BO上截取BN=OM=2,则ME=EN,AF=FM,则EF=$\frac{1}{2}$AN,求出AN即可解决问题.
解答 解:如图,当点Q与O重合,点P与B重合,此时点C与OB的中点E重合,
当点Q与A重合时,点P在点M处,BM=OA=6,此时点C在AM的中点F处,由此可知点C的运动轨迹是线段FE(红线),
在BO上截取BN=OM=2,则ME=EN,AF=FM,
∴EF=$\frac{1}{2}$AN,
在Rt△AON中,AN=$\sqrt{O{A}^{2}+O{N}^{2}}$=$\sqrt{{6}^{2}+{6}^{2}}$=6$\sqrt{2}$,
∴EF=$\frac{1}{2}$AN=3$\sqrt{2}$,
∴点C的运动轨迹的长为3$\sqrt{2}$,
故答案为3$\sqrt{2}$.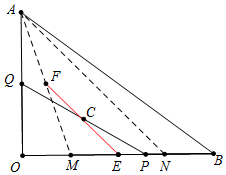
点评 本题考查勾股定理,轨迹等知识,判断出点C运动的路径是线段EF是解题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
9.点P(a+b,2a-b)与点Q(-2,-3)关于y轴对称,则a+b的值是( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | -2 | D. | 2 |
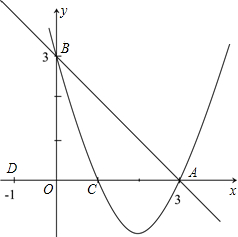 如图,已知C点的坐标为(1,0),直线y=-x+3交于x轴于点A,交y轴于点B,抛物线y=ax2+bx+c经过A,B,C三点.
如图,已知C点的坐标为(1,0),直线y=-x+3交于x轴于点A,交y轴于点B,抛物线y=ax2+bx+c经过A,B,C三点.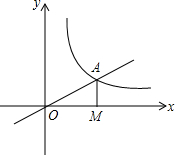 如图所示,正比例函数y=$\frac{1}{2}$x的图象与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象交于点A,过点A作x轴的垂线,垂足为M,已知△OAM的面积为1.
如图所示,正比例函数y=$\frac{1}{2}$x的图象与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象交于点A,过点A作x轴的垂线,垂足为M,已知△OAM的面积为1.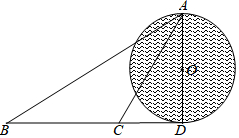 如图,某小岛受到了污染,污染范围可以大致看成是以点O为圆心,AD长为直径的圆形区域,为了测量受污染的圆形区域的直径,在对应⊙O的切线BD(点D为切点)上选择相距300米的B、C两点,分别测得∠ABD=30°,∠ACD=60°.
如图,某小岛受到了污染,污染范围可以大致看成是以点O为圆心,AD长为直径的圆形区域,为了测量受污染的圆形区域的直径,在对应⊙O的切线BD(点D为切点)上选择相距300米的B、C两点,分别测得∠ABD=30°,∠ACD=60°.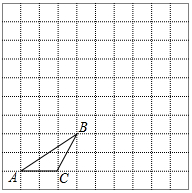 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点).
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点).