题目内容
7.如图1,在△ABC中,点D为边AC上一点,且∠DBC=∠BAC.(1)求证:BC2=CD•AC;
(2)如图2,点E、G分别是BC,DC边上一点,连接AE交BD于点F,连接EG,且∠BDC+∠AEG=180°,
①若点E为BC中点,$\frac{EG}{EF}=\frac{1}{\sqrt{5}}$,求$\frac{AB}{BC}$的值;
②若$\frac{BE}{CE}=\frac{1}{n}$,$\frac{EG}{EF}=\frac{1}{k}$,求$\frac{AB}{BC}$的值(用含n,k的式子表示)
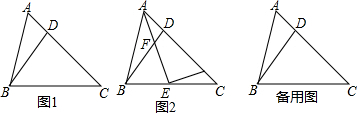
分析 (1)只要证明△CBD∽△CAB即可解决问题;
(2)如图2中,连接DE,作EM⊥BD于M,EN⊥CD于N.首先证明△EMF∽△ENG,推出$\frac{EM}{EN}$=$\frac{EF}{EG}$=$\sqrt{5}$,由BE=EC,推出S△BED=S△ECD,推出$\frac{1}{2}$•BD•EM=$\frac{1}{2}$•DC•EN,推出$\frac{BD}{DC}$=$\frac{EN}{EM}$=$\frac{\sqrt{5}}{5}$,由△CBD∽△CAB,可得$\frac{BD}{AB}$=$\frac{CD}{CB}$,推出$\frac{AB}{BC}$=$\frac{BD}{CD}$,由此即可解决问题.
(3)如图3中,连接DE,作EM⊥BD于M,EN⊥CD于N.首先证明△EMF∽△ENG,推出$\frac{EM}{EN}$=$\frac{EF}{EG}$=k,由BE=nEC,推出S△BED=nS△ECD,推出$\frac{1}{2}$•BD•EM=$\frac{1}{2}$•DC•EN,推出$\frac{BD}{DC}$=n•$\frac{EN}{EM}$=$\frac{n}{k}$,由△CBD∽△CAB,可得$\frac{BD}{AB}$=$\frac{CD}{CB}$,推出$\frac{AB}{BC}$=$\frac{BD}{CD}$,由此即可解决问题.
解答 (1)证明:如图1中,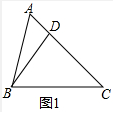
∵∠C=∠C,∠DBC=∠BAC,
∴△CBD∽△CAB,
∴$\frac{CB}{CA}$=$\frac{CD}{CB}$,
∴BC2=CD•AC.
(2)解:如图2中,连接DE,作EM⊥BD于M,EN⊥CD于N.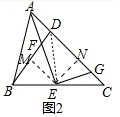
在四边形DFEG中,∵∠FDG+∠FEG=180°,
∴∠DFE+∠DGE=180°,∵∠EFM+∠DFE=180°,
∴∠EFM=∠EGN,
∵∠EMF=∠ENG=90°,
∴△EMF∽△ENG,
∴$\frac{EM}{EN}$=$\frac{EF}{EG}$=$\sqrt{5}$,
∵BE=EC,
∴S△BED=S△ECD,
∴$\frac{1}{2}$•BD•EM=$\frac{1}{2}$•DC•EN,
∴$\frac{BD}{DC}$=$\frac{EN}{EM}$=$\frac{\sqrt{5}}{5}$,
∵△CBD∽△CAB,
∴$\frac{BD}{AB}$=$\frac{CD}{CB}$,
∴$\frac{AB}{BC}$=$\frac{BD}{CD}$=$\frac{\sqrt{5}}{5}$
(3)如图3中,连接DE,作EM⊥BD于M,EN⊥CD于N.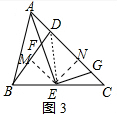
在四边形DFEG中,∵∠FDG+∠FEG=180°,
∴∠DFE+∠DGE=180°,∵∠EFM+∠DFE=180°,
∴∠EFM=∠EGN,
∵∠EMF=∠ENG=90°,
∴△EMF∽△ENG,
∴$\frac{EM}{EN}$=$\frac{EF}{EG}$=K
∵BE=nEC,
∴S△BED=nS△ECD,
∴$\frac{1}{2}$•BD•EM=n$\frac{1}{2}$•DC•EN,
∴$\frac{BD}{DC}$=n•$\frac{EN}{EM}$=$\frac{n}{k}$
∵△CBD∽△CAB,
∴$\frac{BD}{AB}$=$\frac{CD}{CB}$,
∴$\frac{AB}{BC}$=$\frac{BD}{CD}$=$\frac{n}{k}$.
点评 本题考查相似形综合题、相似三角形的判定和性质、三角形的面积等知识,解题的关键是学会添加常用辅助线,构造相似三角形解决问题,学会用转化的首先思考问题,属于中考压轴题.

 如图,在平面直角坐标系中,以原点O为圆心的同心圆的半径由内向外依次为1,2,3,4,…,同心圆与直线y=x和y=-x分别交于A1,A2,A3,A4,…,则A30的坐标是( )
如图,在平面直角坐标系中,以原点O为圆心的同心圆的半径由内向外依次为1,2,3,4,…,同心圆与直线y=x和y=-x分别交于A1,A2,A3,A4,…,则A30的坐标是( )| A. | (4$\sqrt{2}$,-4$\sqrt{2}$) | B. | (-4$\sqrt{2}$,4$\sqrt{2}$) | C. | (-8$\sqrt{2}$,8$\sqrt{2}$) | D. | (30,30) |
 如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于点A﹙-2,-5﹚,C﹙5,n),交y轴于点B,交x轴于点D.
如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于点A﹙-2,-5﹚,C﹙5,n),交y轴于点B,交x轴于点D. 2016年11月-2017年4月某省“共享单车”的用户使用情况如图,根据统计表中提供的信息,预估2017年5月该省共享单车的使用用户约3400万人,你的预估理由是与3-4月份增幅持平.
2016年11月-2017年4月某省“共享单车”的用户使用情况如图,根据统计表中提供的信息,预估2017年5月该省共享单车的使用用户约3400万人,你的预估理由是与3-4月份增幅持平.
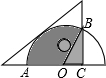 将一块三角板和半圆形量角器按图中方式叠放,重叠部分(阴影)的量角器的圆弧AB对应的圆心角∠AOB=120°,OC=2cm,则图中阴影部分的面积为($\frac{16π}{3}$+2$\sqrt{3}$)cm2.
将一块三角板和半圆形量角器按图中方式叠放,重叠部分(阴影)的量角器的圆弧AB对应的圆心角∠AOB=120°,OC=2cm,则图中阴影部分的面积为($\frac{16π}{3}$+2$\sqrt{3}$)cm2. 如图,Rt△OAB中,∠AOB=90°,OA=6,OB=8,P、Q分别是OB、OA上的动点,满足BP=OQ,C为PQ中点,当Q从O点运动到点A点时,则C点所走过的路径长为3$\sqrt{2}$.
如图,Rt△OAB中,∠AOB=90°,OA=6,OB=8,P、Q分别是OB、OA上的动点,满足BP=OQ,C为PQ中点,当Q从O点运动到点A点时,则C点所走过的路径长为3$\sqrt{2}$.