题目内容
6.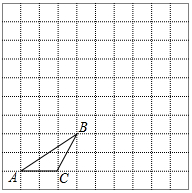 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点).
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点).(1)将△ABC绕点B顺时针旋转90°得到△A′BC′,请画出△A′BC′,并求BA边旋转到BA′位置时所扫过图形的面积;
(2)请在网格中画出一个格点△A″B″C″,使△A″B″C″∽△ABC,且相似比为2.
分析 (1)利用网格特点和旋转的性质画出点A、C的对应点A′、C′,从而得到△A′BC′,然后利用弧长公式计算BA边旋转到BA′位置时所扫过图形的面积;
(2)分别以△ABC的各边的2倍画格点△A″B″C″即可.
解答 解:(1)如图,△A′BC′为所作;
AB=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$,
所以BA边旋转到BA′位置时所扫过图形的面积=$\frac{90•π•\sqrt{13}}{180}$=$\frac{\sqrt{13}}{2}$π;
(2)如图,△A″B″C″为所作.
点评 本题考查了作图-相似变换:两个图形相似,其中一个图形可以看作由另一个图形放大或缩小得到.也考查了旋转变换.

练习册系列答案
相关题目
17. 如图,Rt△OAB中,∠AOB=90°,OA=6,OB=8,P、Q分别是OB、OA上的动点,满足BP=OQ,C为PQ中点,当Q从O点运动到点A点时,则C点所走过的路径长为3$\sqrt{2}$.
如图,Rt△OAB中,∠AOB=90°,OA=6,OB=8,P、Q分别是OB、OA上的动点,满足BP=OQ,C为PQ中点,当Q从O点运动到点A点时,则C点所走过的路径长为3$\sqrt{2}$.
 如图,Rt△OAB中,∠AOB=90°,OA=6,OB=8,P、Q分别是OB、OA上的动点,满足BP=OQ,C为PQ中点,当Q从O点运动到点A点时,则C点所走过的路径长为3$\sqrt{2}$.
如图,Rt△OAB中,∠AOB=90°,OA=6,OB=8,P、Q分别是OB、OA上的动点,满足BP=OQ,C为PQ中点,当Q从O点运动到点A点时,则C点所走过的路径长为3$\sqrt{2}$.
18.立方等于8的数是( )
| A. | 4 | B. | 2 | C. | ±2 | D. | ±4 |
16. 如图,在数轴上,点P对应的实数是( )
如图,在数轴上,点P对应的实数是( )
 如图,在数轴上,点P对应的实数是( )
如图,在数轴上,点P对应的实数是( )| A. | $\sqrt{2}$ | B. | $\sqrt{5}$ | C. | π | D. | -1.5 |
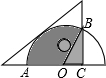 将一块三角板和半圆形量角器按图中方式叠放,重叠部分(阴影)的量角器的圆弧AB对应的圆心角∠AOB=120°,OC=2cm,则图中阴影部分的面积为($\frac{16π}{3}$+2$\sqrt{3}$)cm2.
将一块三角板和半圆形量角器按图中方式叠放,重叠部分(阴影)的量角器的圆弧AB对应的圆心角∠AOB=120°,OC=2cm,则图中阴影部分的面积为($\frac{16π}{3}$+2$\sqrt{3}$)cm2.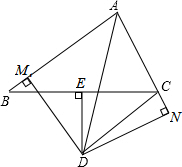 如图:△ABC中,DE是BC边的垂直平分线,垂足为E,AD平分∠BAC且MD⊥AB,DN⊥AC延长线于N.求证:BM=CN.
如图:△ABC中,DE是BC边的垂直平分线,垂足为E,AD平分∠BAC且MD⊥AB,DN⊥AC延长线于N.求证:BM=CN.