题目内容
2.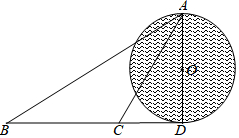 如图,某小岛受到了污染,污染范围可以大致看成是以点O为圆心,AD长为直径的圆形区域,为了测量受污染的圆形区域的直径,在对应⊙O的切线BD(点D为切点)上选择相距300米的B、C两点,分别测得∠ABD=30°,∠ACD=60°.
如图,某小岛受到了污染,污染范围可以大致看成是以点O为圆心,AD长为直径的圆形区域,为了测量受污染的圆形区域的直径,在对应⊙O的切线BD(点D为切点)上选择相距300米的B、C两点,分别测得∠ABD=30°,∠ACD=60°.求:
(1)直径AD长为多少米.
(2)污染范围的面积是多少?
(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
(注意:中间过程用两位小数,每问结果均保留整数)
分析 (1)先利用切线的性质得∠ADB=90°,再利用正切的定义得到DB=$\frac{AD}{tan30°}$=$\sqrt{3}$AD,CD=$\frac{AD}{tan60°}$=$\frac{\sqrt{3}}{3}$AD,则利用DB-CD=300得到AD-$\frac{\sqrt{3}}{3}$AD=300,于是可计算出AD的长;
(2)根据圆的面积公式计算.
解答 解:∵AD为⊙O的直径,BD为⊙O的切线,
∴AD⊥BD,∠ADB=90°,
∵BC=300米,∠ABD=30°,∠ACD=60°,
∴在Rt△ADB和Rt△ADC中,
DB=$\frac{AD}{tan30°}$=$\sqrt{3}$AD,CD=$\frac{AD}{tan60°}$=$\frac{\sqrt{3}}{3}$AD,
∵DB-CD=300,$\sqrt{3}$AD-$\frac{\sqrt{3}}{3}$AD=300,
∴AD=15$\sqrt{3}$≈150×1.73=259.5≈260(米);
(2)污染范围是⊙O的面积=π•OA2=3.14×1302≈5306.6≈5307(米2).
即⊙O直径为260米,被污染范围的面积为5307米2.
点评 本题考查了解直角三角形:将实际问题抽象为数学问题(画出平面图形,构造出直角三角形转化为解直角三角形问题).根据题目已知特点选用适当锐角三角函数或边角关系去解直角三角形,得到数学问题的答案,再转化得到实际问题的答案.也考查了切线的性质.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
10. 如图,AB是⊙O的弦,AC是⊙O的切线,A为切点,BC经过圆心.若∠C=50°,则∠B的大小等于( )
如图,AB是⊙O的弦,AC是⊙O的切线,A为切点,BC经过圆心.若∠C=50°,则∠B的大小等于( )
 如图,AB是⊙O的弦,AC是⊙O的切线,A为切点,BC经过圆心.若∠C=50°,则∠B的大小等于( )
如图,AB是⊙O的弦,AC是⊙O的切线,A为切点,BC经过圆心.若∠C=50°,则∠B的大小等于( )| A. | 20° | B. | 25° | C. | 40° | D. | 50° |
17. 如图,Rt△OAB中,∠AOB=90°,OA=6,OB=8,P、Q分别是OB、OA上的动点,满足BP=OQ,C为PQ中点,当Q从O点运动到点A点时,则C点所走过的路径长为3$\sqrt{2}$.
如图,Rt△OAB中,∠AOB=90°,OA=6,OB=8,P、Q分别是OB、OA上的动点,满足BP=OQ,C为PQ中点,当Q从O点运动到点A点时,则C点所走过的路径长为3$\sqrt{2}$.
 如图,Rt△OAB中,∠AOB=90°,OA=6,OB=8,P、Q分别是OB、OA上的动点,满足BP=OQ,C为PQ中点,当Q从O点运动到点A点时,则C点所走过的路径长为3$\sqrt{2}$.
如图,Rt△OAB中,∠AOB=90°,OA=6,OB=8,P、Q分别是OB、OA上的动点,满足BP=OQ,C为PQ中点,当Q从O点运动到点A点时,则C点所走过的路径长为3$\sqrt{2}$.
7.下列计算正确的是( )
| A. | b3•b3=2b3 | B. | (a3)2•a4=a10 | C. | (ab2)3=ab6 | D. | (-2a)2=-4a2 |
 2016年11月-2017年4月某省“共享单车”的用户使用情况如图,根据统计表中提供的信息,预估2017年5月该省共享单车的使用用户约3400万人,你的预估理由是与3-4月份增幅持平.
2016年11月-2017年4月某省“共享单车”的用户使用情况如图,根据统计表中提供的信息,预估2017年5月该省共享单车的使用用户约3400万人,你的预估理由是与3-4月份增幅持平.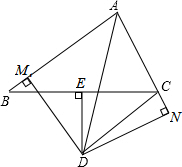 如图:△ABC中,DE是BC边的垂直平分线,垂足为E,AD平分∠BAC且MD⊥AB,DN⊥AC延长线于N.求证:BM=CN.
如图:△ABC中,DE是BC边的垂直平分线,垂足为E,AD平分∠BAC且MD⊥AB,DN⊥AC延长线于N.求证:BM=CN.