题目内容
12.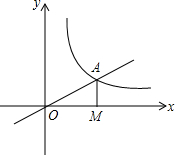 如图所示,正比例函数y=$\frac{1}{2}$x的图象与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象交于点A,过点A作x轴的垂线,垂足为M,已知△OAM的面积为1.
如图所示,正比例函数y=$\frac{1}{2}$x的图象与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象交于点A,过点A作x轴的垂线,垂足为M,已知△OAM的面积为1.(1)求反比例函数的解析式;
(2)如果点B为反比例函数在第一象限图象上的点(点B与点A不重合),且点B的横坐标为1,在x轴上求一点P,使PA+PB最小.
分析 (1)先求出点A的坐标,然后将点A的坐标代入反比例函数的解析式中即可求出k的值.
(2)求出点A关于x轴的对称点C,然后连接BC交于x轴于点P,求出直线BC的解析式后即可求出点P的坐标.
解答 解:(1)设点A(x,y)
∵△OAM的面积为1,
∴$\frac{1}{2}$xy=1,
∵y=$\frac{1}{2}$x,
∴解得:x=±2,
∵x>0,
∴y=1,
∴点A(2,1),
将点A的坐标代入y=$\frac{k}{x}$,
∴k=2,
∴反比例函数的解析式为:y=$\frac{2}{x}$,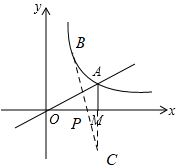
(2)将x=1代入y=$\frac{2}{x}$,
∴y=2,
∴B(1,2),
设点A关于x轴的对称点为C,连接BC交x轴于点P,
∴点C(2,-1),
设直线BC的解析式为:y=mx+n,
将点B(1,2)和C(2,-1)代入y=mx+n,
∴$\left\{\begin{array}{l}{2=m+n}\\{-1=2m+n}\end{array}\right.$
解得:$\left\{\begin{array}{l}{m=-3}\\{n=5}\end{array}\right.$
∴直线BC的解析式为:y=-3x+5
令y=0,
∴x=$\frac{5}{3}$
∴当点P($\frac{5}{3}$,0)时,此时PA+PB最小.
点评 本题考查一次函数与反比例函数的综合问题,解题的关键是熟练运用解方程,待定系数法等知识,本题属于中等题型.

练习册系列答案
相关题目
2.我们用[a]表示不大于a的最大整数,例如:[2.5]=2,[3]=3,[-2.5]=-3.已知x、y满足方程组$\left\{\begin{array}{l}{3[x]+2[y]=9}\\{3[x]-[y]=0}\end{array}\right.$,则[x+y]可能的值有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
17. 如图,Rt△OAB中,∠AOB=90°,OA=6,OB=8,P、Q分别是OB、OA上的动点,满足BP=OQ,C为PQ中点,当Q从O点运动到点A点时,则C点所走过的路径长为3$\sqrt{2}$.
如图,Rt△OAB中,∠AOB=90°,OA=6,OB=8,P、Q分别是OB、OA上的动点,满足BP=OQ,C为PQ中点,当Q从O点运动到点A点时,则C点所走过的路径长为3$\sqrt{2}$.
 如图,Rt△OAB中,∠AOB=90°,OA=6,OB=8,P、Q分别是OB、OA上的动点,满足BP=OQ,C为PQ中点,当Q从O点运动到点A点时,则C点所走过的路径长为3$\sqrt{2}$.
如图,Rt△OAB中,∠AOB=90°,OA=6,OB=8,P、Q分别是OB、OA上的动点,满足BP=OQ,C为PQ中点,当Q从O点运动到点A点时,则C点所走过的路径长为3$\sqrt{2}$.
2. 如图是一个长18cm,宽15cm的矩形图案,其中有两条宽度相等,互相垂直的彩条,彩条所占面积是图案面积的三分之一.设彩条的宽度为x cm,则下列方程正确的是( )
如图是一个长18cm,宽15cm的矩形图案,其中有两条宽度相等,互相垂直的彩条,彩条所占面积是图案面积的三分之一.设彩条的宽度为x cm,则下列方程正确的是( )
 如图是一个长18cm,宽15cm的矩形图案,其中有两条宽度相等,互相垂直的彩条,彩条所占面积是图案面积的三分之一.设彩条的宽度为x cm,则下列方程正确的是( )
如图是一个长18cm,宽15cm的矩形图案,其中有两条宽度相等,互相垂直的彩条,彩条所占面积是图案面积的三分之一.设彩条的宽度为x cm,则下列方程正确的是( )| A. | 18x+15x-x2=$\frac{1}{3}$×15×18 | B. | (18-x)(15-x)=$\frac{1}{3}$×15×18 | ||
| C. | 18x+15x=$\frac{1}{3}$×15×18 | D. | 18x+15x+x2=$\frac{1}{3}$×15×18 |
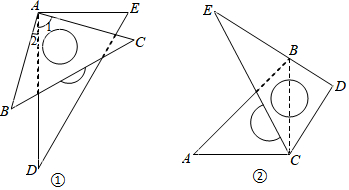
 如图,在四边形ABCD中,∠B=90°,E为AB上一点,分别以ED,EC为折痕将两个角(∠A,∠B)向内折起,点A,B恰好落在CD边的点F处,若AD=3,BC=5.
如图,在四边形ABCD中,∠B=90°,E为AB上一点,分别以ED,EC为折痕将两个角(∠A,∠B)向内折起,点A,B恰好落在CD边的点F处,若AD=3,BC=5. 如图,AB是半圆O的直径,C是半圆上一点.以O为圆心,OE长为半径的半圆交AB于E、F两点,D是其上一动点(可以与E、F两点重合),CD是小半圆的切线,D为切点.已知AO=4,EO=2,设阴影部分的面积为S,则S的取值范围是2$\sqrt{3}$-$\frac{2π}{3}$≤S≤$\frac{20π}{3}$-2$\sqrt{3}$.
如图,AB是半圆O的直径,C是半圆上一点.以O为圆心,OE长为半径的半圆交AB于E、F两点,D是其上一动点(可以与E、F两点重合),CD是小半圆的切线,D为切点.已知AO=4,EO=2,设阴影部分的面积为S,则S的取值范围是2$\sqrt{3}$-$\frac{2π}{3}$≤S≤$\frac{20π}{3}$-2$\sqrt{3}$.