题目内容
8.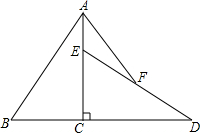 如图,已知Rt△ABC中,∠ACB=90°,AC=12,BC=8,将△ABC绕直角顶点C顺时针旋转90°得到△DEC.若点F是DE的中点,连接AF,则AF=10.
如图,已知Rt△ABC中,∠ACB=90°,AC=12,BC=8,将△ABC绕直角顶点C顺时针旋转90°得到△DEC.若点F是DE的中点,连接AF,则AF=10.
分析 先依据旋转的性质得到CE、CD的长,然后过点F作FG⊥AC,从而可证明FG是△ECD的中位线,从而可得到EG、FG的长,最后依据勾股定理可求得AF的长.
解答 解:如图所示:过点F作FG⊥AC于G.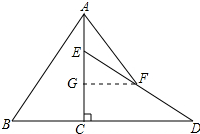
由旋转的性质可知:CE=BC=8,CD=AC=12,∠ECD=∠BCA=90°.
∴AE=AC-CE=4.
∵FG⊥AC,CD⊥AC,
∴FG∥CD.
又∵F是ED的中点,
∴G是CE的中点,
∴EG=4,FG=$\frac{1}{2}$CD=6.
∴AG=AE+EG=8.
∴AF=$\sqrt{A{G}^{2}+F{G}^{2}}$=$\sqrt{{8}^{2}+{6}^{2}}$=10.
故答案为:10.
点评 本题主要考查的是旋转的性质、平行线分线段成比例定理、三角形的中位线定理、勾股定理的应用,证得FG为△△ECD的中位线是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.若式子$\frac{\sqrt{m+1}}{m-1}$在实数范围内有意义,则m的取值范围为( )
| A. | m>1 | B. | m≥-1且m≠1 | C. | m≥-1 | D. | m>-1且m≠1 |
19. 如图,在平面直接坐标系中,有若干个横坐标分别为整数的点,其顺序按图中(1,0)→(2,0)→(2,1)→(1,1)→(1,2)→(2,2)…根据这个规律,则第2016个点的横坐标为( )
如图,在平面直接坐标系中,有若干个横坐标分别为整数的点,其顺序按图中(1,0)→(2,0)→(2,1)→(1,1)→(1,2)→(2,2)…根据这个规律,则第2016个点的横坐标为( )
 如图,在平面直接坐标系中,有若干个横坐标分别为整数的点,其顺序按图中(1,0)→(2,0)→(2,1)→(1,1)→(1,2)→(2,2)…根据这个规律,则第2016个点的横坐标为( )
如图,在平面直接坐标系中,有若干个横坐标分别为整数的点,其顺序按图中(1,0)→(2,0)→(2,1)→(1,1)→(1,2)→(2,2)…根据这个规律,则第2016个点的横坐标为( )| A. | 44 | B. | 45 | C. | 46 | D. | 47 |
16.如图,小明用四张长方形或正方形纸片拼成一个大长方形,小亮根据小明的拼图过程,写出多项式x2+3x+2因式分解的结果为(x+1)(x+2),这个解题过程体现的数学思想主要是( )


| A. | 分类讨论 | B. | 数形结合 | C. | 公理化 | D. | 演绎 |
3.下列结论中,错误的是( )
| A. | 若$\frac{a}{4}$=$\frac{c}{5}$,则$\frac{a}{c}$=$\frac{4}{5}$ | B. | 若$\frac{a-b}{b}$=$\frac{1}{6}$,则$\frac{a}{b}$=$\frac{7}{6}$ | ||
| C. | 若$\frac{a}{b}$=$\frac{c}{d}$=$\frac{2}{3}$(b-d≠0),则$\frac{a-c}{b-d}$=$\frac{2}{3}$ | D. | 若$\frac{a}{b}$=$\frac{3}{4}$,则a=3,b=4 |
20.在下列四个数中,比0小的数是( )
| A. | $\root{3}{-8}$ | B. | |-0.5| | C. | 11% | D. | $\sqrt{3}$ |
17.一个圆锥的高为8cm,底面圆的半径为6cm,则这个圆锥的侧面积为( )
| A. | 20πcm2 | B. | 30πcm2 | C. | 40πcm2 | D. | 60πcm2 |