题目内容
3.下列结论中,错误的是( )| A. | 若$\frac{a}{4}$=$\frac{c}{5}$,则$\frac{a}{c}$=$\frac{4}{5}$ | B. | 若$\frac{a-b}{b}$=$\frac{1}{6}$,则$\frac{a}{b}$=$\frac{7}{6}$ | ||
| C. | 若$\frac{a}{b}$=$\frac{c}{d}$=$\frac{2}{3}$(b-d≠0),则$\frac{a-c}{b-d}$=$\frac{2}{3}$ | D. | 若$\frac{a}{b}$=$\frac{3}{4}$,则a=3,b=4 |
分析 分别利用比例的基本性质分析得出答案.
解答 解:A、若$\frac{a}{4}$=$\frac{c}{5}$,则$\frac{a}{c}$=$\frac{4}{5}$,正确,不合题意;
B、若$\frac{a-b}{b}$=$\frac{1}{6}$,则6(a-b)=b,故6a=7b,则$\frac{a}{b}$=$\frac{7}{6}$,正确,不合题意;
C、若$\frac{a}{b}$=$\frac{c}{d}$=$\frac{2}{3}$(b-d≠0),则$\frac{a-c}{b-d}$=$\frac{2}{3}$,正确,不合题意;
D、若$\frac{a}{b}$=$\frac{3}{4}$,无法得出a,b的值,故此选项错误,符合题意.
故选:D.
点评 此题主要考查了比例的性质,正确应用内项之积等于外项之积是解题关键.

练习册系列答案
相关题目
13.估计$\sqrt{11}$的值在( )
| A. | 1到2之间 | B. | 2到3之间 | C. | 3到4之间 | D. | 4到5之间 |
14.计算:$\sqrt{2x}$•$\sqrt{\frac{1}{2}xy}$=( )
| A. | $\sqrt{xy}$ | B. | x$\sqrt{y}$ | C. | 2x$\sqrt{y}$ | D. | 4x$\sqrt{y}$ |
11.已知△ABC中,∠C=90°,∠A=60°,a+b=3+$\sqrt{3}$,则a等于( )
| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{3}$+1 | D. | 3 |
18.小杰两手中仅有一只手中有硬币,他让小敏猜哪只手中有硬币.下列说法正确的是( )
| A. | 第一次猜中的概率与重放后第二次猜中的概率不一样 | |
| B. | 第一次猜不中后,小杰重放后再猜1次肯定能猜中 | |
| C. | 第一次猜中后,小杰重放后再猜1次肯定猜不中 | |
| D. | 每次猜中的概率都是0.5 |
15.在△ABC中,∠C=90°,∠B=60°,BC=2,则AC=( )
| A. | 1 | B. | 4 | C. | $2\sqrt{3}$ | D. | $3\sqrt{2}$ |
12.Rt△ABC中,直角边AC=3,BC=4,则斜边AB上的中线AD长为( )
| A. | 5 | B. | 2.4 | C. | 2.5 | D. | 4.8 |
13.下列方程中,是关于x的一元二次方程的为( )
| A. | 4x2=3y | B. | x2+$\frac{1}{x}$=-1 | C. | 2x2=0 | D. | x2=(x-1)(x-2) |
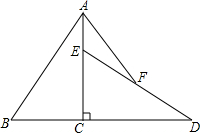 如图,已知Rt△ABC中,∠ACB=90°,AC=12,BC=8,将△ABC绕直角顶点C顺时针旋转90°得到△DEC.若点F是DE的中点,连接AF,则AF=10.
如图,已知Rt△ABC中,∠ACB=90°,AC=12,BC=8,将△ABC绕直角顶点C顺时针旋转90°得到△DEC.若点F是DE的中点,连接AF,则AF=10.