题目内容
13.将抛物线y=2(x+1)2+7绕顶点旋转180°后得到的抛物线的解析式为y=-2(x+1)2+7.分析 当抛物线y=2(x+1)2+7绕其顶点旋转180°后,抛物线的顶点坐标不变,只是开口方向相反,则可根据顶点式写出旋转后的抛物线解析式.
解答 解:抛物线y=2(x+1)2+7的顶点坐标为(-1,7),
由于抛物线y=2(x+1)2+7绕其顶点旋转180°后抛物线的顶点坐标不变,只是开口方向相反,
则所得抛物线解析式为y=-2(x+1)2+7,
故答案为y=-2(x+1)2+7
点评 此题主要考查了根据二次函数的图象的变换求抛物线的解析式,解题的关键是求出旋转后抛物线的顶点坐标.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
3.宜昌市2015年中考学生人数约为2.83万人,近似数2.83万是精确到( )
| A. | 十分位 | B. | 百分位 | C. | 千位 | D. | 百位 |
4.利用加减消元法解方程组$\left\{\begin{array}{l}{3x+4y=16,(1)}\\{5x-6y=14,(2)}\end{array}\right.$,下列做法正确的是( )
| A. | 要消去y,可以将(1)×2+(2)×3 | B. | 要消去x,可以将(1)×3+(2)×(-5) | ||
| C. | 要消去y,可以将(1)×5+(2)×3 | D. | 要消去x,可以将(1)×(-5)+(2)×3 |
1.在-1.4,0,-$\sqrt{2}$,-$\sqrt{5}$这四个数中,比-2小的数是( )
| A. | -1.4 | B. | 0 | C. | -$\sqrt{2}$ | D. | -$\sqrt{5}$ |
18.tan30°的值等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
5. 如图所示零件的左视图是( )
如图所示零件的左视图是( )
 如图所示零件的左视图是( )
如图所示零件的左视图是( )| A. |  | B. |  | C. |  | D. |  |
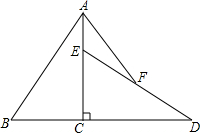 如图,已知Rt△ABC中,∠ACB=90°,AC=12,BC=8,将△ABC绕直角顶点C顺时针旋转90°得到△DEC.若点F是DE的中点,连接AF,则AF=10.
如图,已知Rt△ABC中,∠ACB=90°,AC=12,BC=8,将△ABC绕直角顶点C顺时针旋转90°得到△DEC.若点F是DE的中点,连接AF,则AF=10.



