题目内容
10.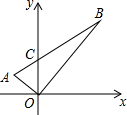 如图,在直角坐标平面上,△AOB是直角三角形,点O在原点上,A、B两点的坐标分别为(-1,y1)、(3,y2),线段AB交y轴于点C.若S△AOC=1,记∠AOC为α,∠BOC为β,则sinα•sinβ的值为$\frac{3}{8}$.
如图,在直角坐标平面上,△AOB是直角三角形,点O在原点上,A、B两点的坐标分别为(-1,y1)、(3,y2),线段AB交y轴于点C.若S△AOC=1,记∠AOC为α,∠BOC为β,则sinα•sinβ的值为$\frac{3}{8}$.
分析 首先过点A作AD⊥x轴于点D,过点B作BE⊥x轴于点E,由A、B两点的坐标分别为(-1,y1)、(3,y2),S△AOC=1,可求得OD,OE,OC的长,继而求得△AOB的面积,求得OA•OB的值,又由三角函数的定义,即可求得答案.
解答  解:过点A作AD⊥x轴于点D,过点B作BE⊥x轴于点E,
解:过点A作AD⊥x轴于点D,过点B作BE⊥x轴于点E,
∵A、B两点的坐标分别为(-1,y1)、(3,y2),
∴OD=1,OE=3,
∵S△AOC=1,
∴$\frac{1}{2}$OC•OD=1,
∴OC=2,
∴SRt△AOB=S△AOC+S△BOC=1+$\frac{1}{2}$OC•OE=1+3=4,
∴$\frac{1}{2}$OA•OB=4,
∴OA•OB=8,
∵OA∥OC∥BE,
∴∠OAD=∠AOC=α,∠OBE=∠BOC=β,
∴sinα•sinβ=$\frac{OD}{OA}$•$\frac{OE}{OB}$=$\frac{OD•OE}{OA•OB}$=$\frac{3}{8}$.
故答案为:$\frac{3}{8}$.
点评 此题考查了三角函数的定义、直角三角形的性质以及坐标与图形的性质.此题难度适中,解题的关键是准确作出辅助线,注意数形结合思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.将分别标有数字0,1,2,3的司长卡片背面朝上洗匀后,抽取一张作为十位上的数字,再抽取一张作为个位上的数字,每次抽取都不放回,则所得的两位数恰好是奇数的概率等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{4}{9}$ | D. | $\frac{5}{9}$ |
18.下列各组数中,互为相反数的是( )
| A. | 3和-3 | B. | 3和-$\frac{1}{3}$ | C. | -3和$\frac{1}{3}$ | D. | 3和$\frac{1}{3}$ |
20.下列方程中,是二元一次方程的为( )
| A. | $x-\frac{1}{x}=3$ | B. | x+xy=-1 | C. | $\frac{x}{3}-\frac{y}{5}=6$ | D. | x2-2x-1=0 |
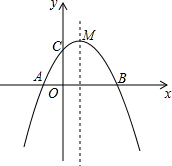 如图,抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C,且OA=OC,M是抛物线的顶点,三角形AMB的面积等于1,则下列结论:
如图,抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C,且OA=OC,M是抛物线的顶点,三角形AMB的面积等于1,则下列结论: 将一张三角形纸片ABC,沿AD进行折叠,点C的对应点E落在△ABC外面,DE交AB于点F,得到如图所示的多边形AEFBD,这个多边形的面积是△ABC面积的$\frac{13}{16}$.已知图中阴影部分的面积为50,则△ABC的面积为80.
将一张三角形纸片ABC,沿AD进行折叠,点C的对应点E落在△ABC外面,DE交AB于点F,得到如图所示的多边形AEFBD,这个多边形的面积是△ABC面积的$\frac{13}{16}$.已知图中阴影部分的面积为50,则△ABC的面积为80.