题目内容
3.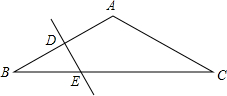 如图,在△ABC中,AB=AC=6cm,∠A=120°,AB的垂直平分线分别交AB,BC于D,E,则EC的长为( )
如图,在△ABC中,AB=AC=6cm,∠A=120°,AB的垂直平分线分别交AB,BC于D,E,则EC的长为( )| A. | 4$\sqrt{3}$cm | B. | 2$\sqrt{3}$cm | C. | 5cm | D. | $\frac{5\sqrt{3}}{2}$cm |
分析 根据等腰三角形两底角相等求出∠B=∠C=30°,连接AE,根据线段垂直平分线上的点到线段两端点的距离相等可得AE=BE,再利用等边对等角求出∠BAE=∠B=30°,然后求出∠CAE=90°,解直角三角形即可得到结论.
解答  解:∵AB=AC,∠A=120°,
解:∵AB=AC,∠A=120°,
∴∠B=∠C=$\frac{1}{2}$(180°-120°)=30°,
连接AE,
∵AB的垂直平分线交BC于E,
∴AE=BE,
∴∠EAB=∠B=30°,
∵∠A=120°,
∴∠EAC=90°,
∴CE=$\frac{AC}{cos30°}$=4$\sqrt{3}$.
点评 本题考查了线段垂直平分线上的点到线段两端点的距离相等的性质,等边对等角的性质,直角三角形30°角所对的直角边等于斜边的一半的性质,熟记性质并作辅助线构造出直角三角形是解题的关键.

练习册系列答案
相关题目
14.已知等腰三角形的两边长为4cm和8cm,则三角形周长是( )
| A. | 12 cm | B. | 16cm | C. | 20cm | D. | 16cm或20cm |
11.下列分解因式正确的是( )
| A. | 2x2+4xy=x(2x+4y) | B. | 4a2-4ab+b2=(2a-b)2 | ||
| C. | x3-x=x(x2-1) | D. | 3x2-5xy+x=x(3x-5y) |
18.甲、乙两个人关于年龄有如下对话,甲说:“我是你现在这个年龄时,你是10岁”.乙说:“我是你现在这个年龄时,你是25岁”.设现在甲x岁,乙y岁,下列方程组正确的是( )
| A. | $\left\{\begin{array}{l}{y-10=x-y}\\{x-y=25-x}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{y-10=x-y}\\{x-y=25-y}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{y-10=x-y}\\{x-y=25+x}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{y+10=x-y}\\{x-y=25-x}\end{array}\right.$ |
12. 如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于(1,0)及(x1,0),且-2<x1<-1,与y轴的交点在(0,2)上方,则下列结论中错误的是( )
如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于(1,0)及(x1,0),且-2<x1<-1,与y轴的交点在(0,2)上方,则下列结论中错误的是( )
 如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于(1,0)及(x1,0),且-2<x1<-1,与y轴的交点在(0,2)上方,则下列结论中错误的是( )
如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于(1,0)及(x1,0),且-2<x1<-1,与y轴的交点在(0,2)上方,则下列结论中错误的是( )| A. | abc>0 | B. | a+b+c=0 | C. | 2a-b>-1 | D. | 2a+c<0 |
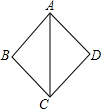 如图,在△ABC和△ADC中,下列结论:
如图,在△ABC和△ADC中,下列结论: