题目内容
12. 如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于(1,0)及(x1,0),且-2<x1<-1,与y轴的交点在(0,2)上方,则下列结论中错误的是( )
如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于(1,0)及(x1,0),且-2<x1<-1,与y轴的交点在(0,2)上方,则下列结论中错误的是( )| A. | abc>0 | B. | a+b+c=0 | C. | 2a-b>-1 | D. | 2a+c<0 |
分析 A、正确.判断出a、b、c的符号即可解决问题.
B、正确.根据x=1时,y=0,即可判断.
C、错误..根据x=-2时,y<0,即可判断.
D、正确.取符合条件-2<x1<-1的任何一个x1,1•x1>-2,由一元二次方程根与系数的关系即可判断.
解答 解:A、正确.∵开口向下,
∴a<0,
∵抛物线交y轴于正半轴,
∴c>0,
∵-$\frac{b}{2a}$<0,
∴b<0,
∴abc>0,故A正确.
B、正确.∵x=1时,y=0,
∴a+b+c=0,故B正确.
C、错误.∵x=-2时,y<0,
∴4a-2b+c<0,
∴2a-b<-$\frac{c}{2}$,
∵c>2,
∴2a-b<-1,故C错误.
D.正确,取符合条件-2<x1<-1的任何一个x1,1•x1>-2,
∴由一元二次方程根与系数的关系知 x1•x2=$\frac{c}{a}$>-2,
∴c<-2a,
∴2a+c<0,故D正确.
故选C.
点评 本题考查二次函数与系数关系,熟练掌握二次函数的性质是解决问题的关键,学会利用图象信息解决问题,题目有难度,属于中考常考题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.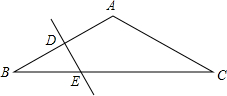 如图,在△ABC中,AB=AC=6cm,∠A=120°,AB的垂直平分线分别交AB,BC于D,E,则EC的长为( )
如图,在△ABC中,AB=AC=6cm,∠A=120°,AB的垂直平分线分别交AB,BC于D,E,则EC的长为( )
 如图,在△ABC中,AB=AC=6cm,∠A=120°,AB的垂直平分线分别交AB,BC于D,E,则EC的长为( )
如图,在△ABC中,AB=AC=6cm,∠A=120°,AB的垂直平分线分别交AB,BC于D,E,则EC的长为( )| A. | 4$\sqrt{3}$cm | B. | 2$\sqrt{3}$cm | C. | 5cm | D. | $\frac{5\sqrt{3}}{2}$cm |
2.方程x2+x-12=0的两个根为( )
| A. | x1=-2,x2=6 | B. | x1=-6,x2=2 | C. | x1=-3,x2=4 | D. | x1=-4,x2=3 |
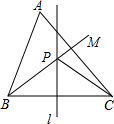 如图,锐角三角形ABC中,直线L为BC的中垂线,射线BM为∠ABC的角平分线,直线l与射线BM相交于P点,若∠A=60°,∠ACP=24°,则∠ABP的度数为32°.
如图,锐角三角形ABC中,直线L为BC的中垂线,射线BM为∠ABC的角平分线,直线l与射线BM相交于P点,若∠A=60°,∠ACP=24°,则∠ABP的度数为32°.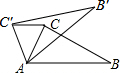 已知:如图,在△ABC中,∠CAB=70°,将△ABC绕点A按逆时针方向旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′的度数为40°.
已知:如图,在△ABC中,∠CAB=70°,将△ABC绕点A按逆时针方向旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′的度数为40°.