题目内容
15.知矩形的对角线长为4cm,其中一条边的长2$\sqrt{3}$cm,则面积为$4\sqrt{3}$cm2.分析 由矩形的性质得出AC=BD=4cm,∠ABC=90°,由勾股定理求出AB的长,再由矩形的面积公式即可得出结果.
解答 解:如图所示:
∵四边形ABCD是矩形,
∴AC=BD=4cm,∠ABC=90°,
∵BC=2$\sqrt{3}$cm,
∴AB=$\sqrt{A{C}^{2}-B{C}^{2}}$=$\sqrt{{4}^{2}-(2\sqrt{3})^{2}}$=2(cm),
∴矩形的面积=AB•BC=2×2$\sqrt{3}$=4$\sqrt{3}$(cm2);
故答案为:4$\sqrt{3}$.
点评 本题考查了矩形的性质、勾股定理;熟练掌握矩形的性质,由勾股定理求出AC是解决问题的关键.

练习册系列答案
相关题目
5.为了了解某校八年级720名学生的提中情况,从中抽查了80名学生的体重进行统计分析,以下说法正确的是( )
| A. | 这80名学生是总体的一个样本 | B. | 80名学生是样本容量 | ||
| C. | 每名学生的体重是个体 | D. | 720名学生是总体 |
3.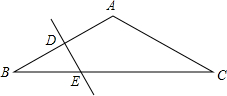 如图,在△ABC中,AB=AC=6cm,∠A=120°,AB的垂直平分线分别交AB,BC于D,E,则EC的长为( )
如图,在△ABC中,AB=AC=6cm,∠A=120°,AB的垂直平分线分别交AB,BC于D,E,则EC的长为( )
 如图,在△ABC中,AB=AC=6cm,∠A=120°,AB的垂直平分线分别交AB,BC于D,E,则EC的长为( )
如图,在△ABC中,AB=AC=6cm,∠A=120°,AB的垂直平分线分别交AB,BC于D,E,则EC的长为( )| A. | 4$\sqrt{3}$cm | B. | 2$\sqrt{3}$cm | C. | 5cm | D. | $\frac{5\sqrt{3}}{2}$cm |
10.下列调查中,适合用普查方式的是( )
| A. | 了解一批炮弹的杀伤半径 | |
| B. | 了解扬州电视台《关注》栏目的收视率 | |
| C. | 了解长江中鱼的种类 | |
| D. | 了解某班学生最喜爱的体育项目 |
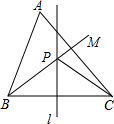 如图,锐角三角形ABC中,直线L为BC的中垂线,射线BM为∠ABC的角平分线,直线l与射线BM相交于P点,若∠A=60°,∠ACP=24°,则∠ABP的度数为32°.
如图,锐角三角形ABC中,直线L为BC的中垂线,射线BM为∠ABC的角平分线,直线l与射线BM相交于P点,若∠A=60°,∠ACP=24°,则∠ABP的度数为32°.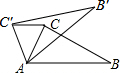 已知:如图,在△ABC中,∠CAB=70°,将△ABC绕点A按逆时针方向旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′的度数为40°.
已知:如图,在△ABC中,∠CAB=70°,将△ABC绕点A按逆时针方向旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′的度数为40°.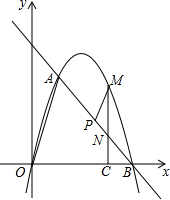 如图,在平面直角坐标系中,点O为坐标原点,直线l与抛物线y=mx2+nx相交于A(1,3$\sqrt{3}$),B(4,0)两点.
如图,在平面直角坐标系中,点O为坐标原点,直线l与抛物线y=mx2+nx相交于A(1,3$\sqrt{3}$),B(4,0)两点.