题目内容
13.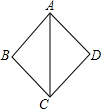 如图,在△ABC和△ADC中,下列结论:
如图,在△ABC和△ADC中,下列结论:①AB=AD;
②∠ABC=∠ADC=90°;
③BC=DC.
把其中两个论断作为条件,另一个论断作为结论,可以写出2个真命题.
分析 共有三种组合:①②⇒③;①③⇒②;②③⇒①,再进行证明即可.
解答 解:①②⇒③;
∵②,
∴在Rt△ABC和Rt△ADC中,
$\left\{\begin{array}{l}{AC=AC}\\{AB=AD}\end{array}\right.$,
∴Rt△ABC≌Rt△ADC,
∴③;
①③⇒②;
在△ABC和△ADC中,
$\left\{\begin{array}{l}{AB=AD}\\{AC=AC}\\{BC=DC}\end{array}\right.$,
∴△ABC≌△ADC,
∴∠ABC=∠ADC,但不一定等于90°,
∴不能推得②;
②③⇒①;
在Rt△ABC和Rt△ADC中,
$\left\{\begin{array}{l}{AC=AC}\\{BC=DC}\end{array}\right.$,
∴Rt△ABC≌Rt△ADC,
∴①;
故答案为2.
点评 本题考查了命题和定理,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.

练习册系列答案
相关题目
3.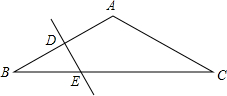 如图,在△ABC中,AB=AC=6cm,∠A=120°,AB的垂直平分线分别交AB,BC于D,E,则EC的长为( )
如图,在△ABC中,AB=AC=6cm,∠A=120°,AB的垂直平分线分别交AB,BC于D,E,则EC的长为( )
 如图,在△ABC中,AB=AC=6cm,∠A=120°,AB的垂直平分线分别交AB,BC于D,E,则EC的长为( )
如图,在△ABC中,AB=AC=6cm,∠A=120°,AB的垂直平分线分别交AB,BC于D,E,则EC的长为( )| A. | 4$\sqrt{3}$cm | B. | 2$\sqrt{3}$cm | C. | 5cm | D. | $\frac{5\sqrt{3}}{2}$cm |
2.方程x2+x-12=0的两个根为( )
| A. | x1=-2,x2=6 | B. | x1=-6,x2=2 | C. | x1=-3,x2=4 | D. | x1=-4,x2=3 |
3.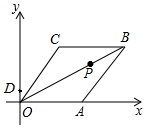 已知菱形OABC在平面直角坐标系的位置如图所示,顶点A(5,0),OB=4$\sqrt{5}$,点P是对角线OB上的一个动点,D(0,1),当CP+DP最短时,点P的坐标为( )
已知菱形OABC在平面直角坐标系的位置如图所示,顶点A(5,0),OB=4$\sqrt{5}$,点P是对角线OB上的一个动点,D(0,1),当CP+DP最短时,点P的坐标为( )
 已知菱形OABC在平面直角坐标系的位置如图所示,顶点A(5,0),OB=4$\sqrt{5}$,点P是对角线OB上的一个动点,D(0,1),当CP+DP最短时,点P的坐标为( )
已知菱形OABC在平面直角坐标系的位置如图所示,顶点A(5,0),OB=4$\sqrt{5}$,点P是对角线OB上的一个动点,D(0,1),当CP+DP最短时,点P的坐标为( )| A. | (0,0) | B. | (1,$\frac{1}{2}$) | C. | ($\frac{6}{5}$,$\frac{3}{5}$) | D. | ($\frac{10}{7}$,$\frac{5}{7}$) |
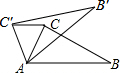 已知:如图,在△ABC中,∠CAB=70°,将△ABC绕点A按逆时针方向旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′的度数为40°.
已知:如图,在△ABC中,∠CAB=70°,将△ABC绕点A按逆时针方向旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′的度数为40°.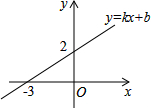 一次函数y=kx+b(k,b是常数,k≠0)的图象如图所示,则不等式kx+b>0的解集是x>-3.
一次函数y=kx+b(k,b是常数,k≠0)的图象如图所示,则不等式kx+b>0的解集是x>-3.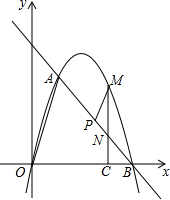 如图,在平面直角坐标系中,点O为坐标原点,直线l与抛物线y=mx2+nx相交于A(1,3$\sqrt{3}$),B(4,0)两点.
如图,在平面直角坐标系中,点O为坐标原点,直线l与抛物线y=mx2+nx相交于A(1,3$\sqrt{3}$),B(4,0)两点.