ΧβΡΩΡΎ»ί
»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§OΈΣΉχ±ξ‘≠ΒψΘ§ΒψA‘Ύy÷α’ΐΑκ÷α…œΘ§ΒψB‘Ύx÷αΗΚΑκ÷α…œΘ§ΒψC‘Ύx÷α’ΐΑκ÷α…œΘ§«“AB=ACΘ§OA=BCΘ§ΒψD «œΏΕΈOA…œ“ΜΒψΘ§«“OD=
OAΘ§ΙΐΒψDΉςx÷αΒΡΤΫ––œΏΫΜœΏΕΈAB”ΎΒψEΘ§ΓςABCΒΡΟφΜΐΈΣ8Θ°
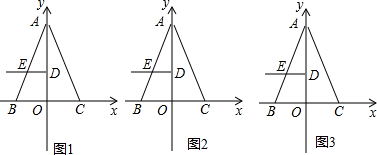
Θ®1Θ©«σABΥυ‘Ύ÷±œΏΒΡΫβΈω Ϋ“‘ΦΑœΏΕΈDEΒΡ≥ΛΘΜ
Θ®2Θ©ΒψP «œΏΕΈOB…œ“ΜΒψΘ®ΒψP≤Μ”κΒψOΓΔB÷ΊΚœΘ©Θ§ΙΐΒψPΉςPQΓΈABΫΜy÷α”ΎΒψQΘ§…ηΒψPΒΡΉχ±ξΈΣΘ®tΘ§0Θ©Θ§œΏΕΈDQ≥ΛΈΣyΘ®yΘΨ0Θ©Θ§«σy”κt÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘ§≤Δ÷±Ϋ”–¥≥ωΉ‘±δΝΩtΒΡ»Γ÷ΒΖΕΈßΘΜ
Θ®3Θ©‘ΎΘ®2Θ©ΒΡΧθΦΰœ¬Θ§M «…δœΏDE…œ“ΜΒψΘ§ «Ζώ¥φ‘Ύt÷ΒΘ§ ΙΓςPMQ «“‘PQΈΣ÷±Ϋ«±ΏΒΡΒ»―ϋ»ΐΫ«–ΈΘΩ»τ¥φ‘Ύ«κ«σ≥ωt÷ΒΦΑΒψMΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
| 1 |
| 4 |

Θ®1Θ©«σABΥυ‘Ύ÷±œΏΒΡΫβΈω Ϋ“‘ΦΑœΏΕΈDEΒΡ≥ΛΘΜ
Θ®2Θ©ΒψP «œΏΕΈOB…œ“ΜΒψΘ®ΒψP≤Μ”κΒψOΓΔB÷ΊΚœΘ©Θ§ΙΐΒψPΉςPQΓΈABΫΜy÷α”ΎΒψQΘ§…ηΒψPΒΡΉχ±ξΈΣΘ®tΘ§0Θ©Θ§œΏΕΈDQ≥ΛΈΣyΘ®yΘΨ0Θ©Θ§«σy”κt÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘ§≤Δ÷±Ϋ”–¥≥ωΉ‘±δΝΩtΒΡ»Γ÷ΒΖΕΈßΘΜ
Θ®3Θ©‘ΎΘ®2Θ©ΒΡΧθΦΰœ¬Θ§M «…δœΏDE…œ“ΜΒψΘ§ «Ζώ¥φ‘Ύt÷ΒΘ§ ΙΓςPMQ «“‘PQΈΣ÷±Ϋ«±ΏΒΡΒ»―ϋ»ΐΫ«–ΈΘΩ»τ¥φ‘Ύ«κ«σ≥ωt÷ΒΦΑΒψMΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
ΩΦΒψΘΚ“Μ¥ΈΚ· ΐΉέΚœΧβ
Ή®ΧβΘΚ
Ζ÷ΈωΘΚΘ®1Θ©ΗυΨί»ΐΫ«–ΈΒΡΟφΜΐΘ§Ω…ΒΟOAΓΔBCΒΡ≥ΛΘ§Ω…ΒΟAΒψBΒψΉχ±ξΘ§ΗυΨί¥ΐΕ®œΒ ΐΖ®Θ§Ω…ΒΟΚ· ΐΫβΈω ΫΘ§ΗυΨίΚ· ΐ÷ΒΘ§Ω…ΒΟœύ”ΠΉ‘±δΝΩΒΡ÷ΒΘΜ
Θ®2Θ©Ζ÷άύΧ÷¬έΘΚΔΌΒ±-2ΘΦtΘΦ-
±Θ§ΔΎΒ±-
ΓήtΘΦ0Θ§ΗυΨίΤΫ––œΏΒΡ–±¬ œύΒ»Θ§Ω…ΒΟPQΒΡΚ· ΐΫβΈω ΫΘ§ΗυΨίΉ‘±δΝΩΒΡ÷ΒΘ§Ω…ΒΟQΒψΒΡΉχ±ξΘ§ΗυΨίPQΒΡΨύάκΘ§Ω…ΒΟΚ· ΐΫβΈω ΫΘΜ
Θ®3Θ©ΗυΨίΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§Ω…ΒΟPQ”κPMΒΡΙΊœΒΘ§ΗυΨίPQΓΆPMΘ§Ω…ΒΟΝΫΧθ÷±œΏΒΡ–±¬ ΒΡ≥ΥΜΐΈΣ-1Θ§‘ΌΗυΨίPQ=PMΘ§Ω…ΒΡΖΫ≥ΧΉιΘ§ΗυΨίΫβΖΫ≥ΧΉιΘ§Ω…ΒΟd¥πΑΗΘ°
Θ®2Θ©Ζ÷άύΧ÷¬έΘΚΔΌΒ±-2ΘΦtΘΦ-
| 1 |
| 2 |
| 1 |
| 2 |
Θ®3Θ©ΗυΨίΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§Ω…ΒΟPQ”κPMΒΡΙΊœΒΘ§ΗυΨίPQΓΆPMΘ§Ω…ΒΟΝΫΧθ÷±œΏΒΡ–±¬ ΒΡ≥ΥΜΐΈΣ-1Θ§‘ΌΗυΨίPQ=PMΘ§Ω…ΒΡΖΫ≥ΧΉιΘ§ΗυΨίΫβΖΫ≥ΧΉιΘ§Ω…ΒΟd¥πΑΗΘ°
Ϋβ¥πΘΚΫβΘΚΘ®1Θ©”…OA=BCΘ§ΓςABCΒΡΟφΜΐΈΣ8Θ§ΒΟ
SΓςABC=
OA•BC=8Θ°
ΫβΒΟOA=BC=4Θ°Φ¥AΘ®0Θ§4Θ©
”…AB=ACΘ§OAΓΆBOΘ§ΒΟ
OB=2Θ§Φ¥BΘ®-2Θ§0Θ©Θ§
…ηABΥυ‘Ύ÷±œΏΒΡΫβΈω ΫΈΣy=kx+bΘ§ΆΦœσΙΐΒψAΓΔBΘ§ΒΟ
Θ§ΫβΒΟ
Θ°
ABΥυ‘Ύ÷±œΏΒΡΫβΈω ΫΈΣy=2x+4Θ§
”…OD=
OA=1Θ§Φ¥DΘ®0Θ§1Θ©Θ°
”…DEΓΈxΘ§ΒΟEΒψΉίΉχ±ξΈΣ1Θ§
Β±y=1 ±Θ§2x+4=1Θ§ΫβΒΟx=-
Θ§
EΘ®-
Θ§1Θ©Θ°
DEΒΡ≥ΛΈΣ0-Θ®-
Θ©=
ΘΜ
Θ®2Θ©»γΆΦ1ΘΚ
ΔΌΒ±-2ΘΦtΘΦ-
±Θ§”…PQΓΈABΘ§…ηPQΒΡΚ· ΐΫβΈω ΫΈΣy=2x+bΘ§
y=0 ±Θ§2t+b=0Θ§ΫβΒΟb=-2tΦ¥QΘ®0Θ§-2tΘ©Θ°
QDΒΡ≥Λy=-2t-1ΘΜ
ΔΎΒ±-
ΓήtΘΦ0 ±Θ§»γΆΦΘΚ Θ§
Θ§
”…PQΓΈABΘ§…ηPQΒΡΚ· ΐΫβΈω ΫΈΣy=2x+bΘ§
y=0 ±Θ§2t+b=0Θ§ΫβΒΟb=-2tΦ¥QΘ®0Θ§-2tΘ©Θ°
QDΒΡ≥Λy=2t+1ΘΜ
Ήέ…œΥυ ωΘΚy=
ΘΜ
Θ®3Θ©»γΆΦ3ΘΚ Θ§
Θ§
…ηQΘ®aΘ§1Θ©Θ§”…Θ®2Θ©ΒΟPΘ®tΘ§0Θ©Θ§QΘ®0Θ§-2tΘ©Θ°
”…ΓςPMQ «“‘PQΈΣ÷±Ϋ«±ΏΒΡΒ»―ϋ»ΐΫ«–ΈΘ§ΒΟQP=PMΘ§QPΓΆPMΘ°
kMP•kPQ=-1Θ°ΒΟkMP=
ΓΝ2=-1Θ°t-a=2ΔΌΘ°
QP2=MQ2Φ¥Θ®-2tΘ©2+t2=Θ®a-tΘ©2+12 ΔΎΘ°
ΝΣΝΔΔΌΔΎΒΟ
Θ§
Μ·ΦρΘ§ΒΟ
Θ§
Α―ΔΌ¥ζ»κΔΎΒΟ5t2=5Θ§ΫβΒΟt=1Θ®≤ΜΖϊΚœΧβ“βΒΡ“Σ…α»ΞΘ©Θ§t=-1Θ§
Α―t=-1¥ζ»κΔΌΒΟa=-1-2=-3Θ§
Φ¥MΘ®-3Θ§1Θ©Θ°
SΓςABC=
| 1 |
| 2 |
ΫβΒΟOA=BC=4Θ°Φ¥AΘ®0Θ§4Θ©
”…AB=ACΘ§OAΓΆBOΘ§ΒΟ
OB=2Θ§Φ¥BΘ®-2Θ§0Θ©Θ§
…ηABΥυ‘Ύ÷±œΏΒΡΫβΈω ΫΈΣy=kx+bΘ§ΆΦœσΙΐΒψAΓΔBΘ§ΒΟ
|
|
ABΥυ‘Ύ÷±œΏΒΡΫβΈω ΫΈΣy=2x+4Θ§
”…OD=
| 1 |
| 4 |
”…DEΓΈxΘ§ΒΟEΒψΉίΉχ±ξΈΣ1Θ§
Β±y=1 ±Θ§2x+4=1Θ§ΫβΒΟx=-
| 3 |
| 2 |
EΘ®-
| 3 |
| 2 |
DEΒΡ≥ΛΈΣ0-Θ®-
| 3 |
| 2 |
| 3 |
| 2 |
Θ®2Θ©»γΆΦ1ΘΚ

ΔΌΒ±-2ΘΦtΘΦ-
| 1 |
| 2 |
y=0 ±Θ§2t+b=0Θ§ΫβΒΟb=-2tΦ¥QΘ®0Θ§-2tΘ©Θ°
QDΒΡ≥Λy=-2t-1ΘΜ
ΔΎΒ±-
| 1 |
| 2 |
 Θ§
Θ§”…PQΓΈABΘ§…ηPQΒΡΚ· ΐΫβΈω ΫΈΣy=2x+bΘ§
y=0 ±Θ§2t+b=0Θ§ΫβΒΟb=-2tΦ¥QΘ®0Θ§-2tΘ©Θ°
QDΒΡ≥Λy=2t+1ΘΜ
Ήέ…œΥυ ωΘΚy=
|
Θ®3Θ©»γΆΦ3ΘΚ
 Θ§
Θ§…ηQΘ®aΘ§1Θ©Θ§”…Θ®2Θ©ΒΟPΘ®tΘ§0Θ©Θ§QΘ®0Θ§-2tΘ©Θ°
”…ΓςPMQ «“‘PQΈΣ÷±Ϋ«±ΏΒΡΒ»―ϋ»ΐΫ«–ΈΘ§ΒΟQP=PMΘ§QPΓΆPMΘ°
kMP•kPQ=-1Θ°ΒΟkMP=
| 1 |
| a-t |
QP2=MQ2Φ¥Θ®-2tΘ©2+t2=Θ®a-tΘ©2+12 ΔΎΘ°
ΝΣΝΔΔΌΔΎΒΟ
|
Μ·ΦρΘ§ΒΟ
|
Α―ΔΌ¥ζ»κΔΎΒΟ5t2=5Θ§ΫβΒΟt=1Θ®≤ΜΖϊΚœΧβ“βΒΡ“Σ…α»ΞΘ©Θ§t=-1Θ§
Α―t=-1¥ζ»κΔΌΒΟa=-1-2=-3Θ§
Φ¥MΘ®-3Θ§1Θ©Θ°
ΒψΤάΘΚ±ΨΧβΩΦ≤ιΝΥ“Μ¥ΈΚ· ΐΉέΚœΧβΘ§Θ®1Θ©άϊ”Ο¥ΐΕ®œΒ ΐΖ®«σΚ· ΐΫβΈω ΫΘ§Θ®2Θ©άϊ”ΟΤΫ––œΏΒΡk÷ΒœύΒ»ΒΟ≥ωPQΚ· ΐΫβΈω Ϋ «ΫβΧβΙΊΦϋΘ§‘ΌΖ÷άύΧ÷¬έΒΟ≥ωΚ· ΐy”κtΒΡΫβΈω ΫΘ§Θ®3Θ©άϊ”Ο¥ΙœΏΒΡk÷ΒΒΡ≥ΥΜΐΈΣ-1Θ§Β»―ϋ»ΐΫ«–ΈΒΡΕ®“εΘ§ΒΟ≥ωΖΫ≥ΧΉι «ΫβΧβΙΊΦϋΘ°

ΝΖœΑ≤αœΒΝ–¥πΑΗ
 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
œύΙΊΧβΡΩ
–ΓΟςΓΔ–ΓΜΔΓΔ–ΓΚλ»ΐ»Υ≈≈≥…“Μ≈≈≈Ρ’’Τ§Θ§–ΓΟς’Ψ‘Ύ÷–ΦδΒΡΗ≈¬ «Θ®ΓΓΓΓΘ©
AΓΔ
| ||
BΓΔ
| ||
CΓΔ
| ||
DΓΔ
|
»τm”κnΈΣ’ΐ’ϊ ΐΘ§xm+yn+2m+nΒΡ¥Έ ΐ «Θ®ΓΓΓΓΘ©
| AΓΔm | BΓΔn |
| CΓΔm+n | DΓΔmΘ§n÷–Ϋœ¥σΒΡ ΐ |
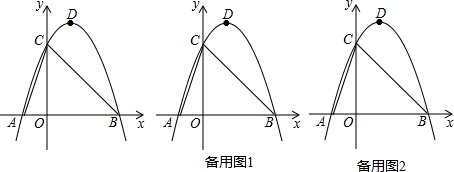
 »γΆΦΘ§ΒψE «ΨΊ–ΈABCD÷–CD±Ώ…œ“ΜΒψΘ§ΓςBCE―ΊBE’έΒΰΈΣΓςBFEΘ§ΒψF¬δ‘ΎAD…œΘ§AB=3Θ§BC=5Θ§tanΓœAFB=
»γΆΦΘ§ΒψE «ΨΊ–ΈABCD÷–CD±Ώ…œ“ΜΒψΘ§ΓςBCE―ΊBE’έΒΰΈΣΓςBFEΘ§ΒψF¬δ‘ΎAD…œΘ§AB=3Θ§BC=5Θ§tanΓœAFB=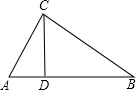 »γΆΦΘ§‘ΎΓςABC÷–Θ§ΓœACB=90ΓψΘ§CDΓΆAB”ΎΒψDΘ§AD=1Θ§BD=4Θ§«σACΒΡ≥ΛΘ°
»γΆΦΘ§‘ΎΓςABC÷–Θ§ΓœACB=90ΓψΘ§CDΓΆAB”ΎΒψDΘ§AD=1Θ§BD=4Θ§«σACΒΡ≥ΛΘ°