已知矩形ABCD的边AB=6.AD=8．如果以点A为圆心作⊙O.使B.C.D三点中在圆内和在圆外都至少有一个点.那么⊙O的半径r的取值范围是．题目和参考答案——青夏教育精英家教网—

题目内容

已知矩形ABCD的边AB=6，AD=8．如果以点A为圆心作⊙O，使B、C、D三点中在圆内和在圆外都至少有一个点，那么⊙O的半径r的取值范围是

．

考点：点与圆的位置关系

专题：

分析：四边形ABCD是矩形，则△ABC是直角三角形．根据勾股定理得到：AC=10，B，C，D三点中在圆内和在圆外都至少有一个点，由题意可知一定是B在圆内，则半径r＞6，一定是点C在圆外，则半径r＜10，所以6＜r＜10．

解答：解：∵AB=6，AD=8，
∴AC=10，
∴点C一定在圆外，点B一定在圆内，
∴⊙O的半径r的取值范围是：6＜r＜10．
故答案为：6＜r＜10．

点评：本题主要考查了勾股定理，以及点和圆的位置关系，可以通过点到圆心的距离与圆的半径比较大小，判定点和圆的位置关系．

练习册系列答案

相关题目

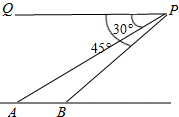青海玉树地震后，抢险队派一架直升机去A，B两个村庄抢险，直升机在上空500m的P处测得A村的俯角为30°，B村的俯角为45°，如图，求A，B两个村庄之间的距离．（结果精确到1m）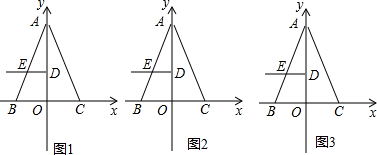

如图，在平面直角坐标系中，O为坐标原点，点A在y轴正半轴上，点B在x轴负半轴上，点C在x轴正半轴上，且AB=AC，OA=BC，点D是线段OA上一点，且OD=

OA，过点D作x轴的平行线交线段AB于点E，△ABC的面积为8．

（1）求AB所在直线的解析式以及线段DE的长；
（2）点P是线段OB上一点（点P不与点O、B重合），过点P作PQ∥AB交y轴于点Q，设点P的坐标为（t，0），线段DQ长为y（y＞0），求y与t之间的函数关系式，并直接写出自变量t的取值范围；
（3）在（2）的条件下，M是射线DE上一点，是否存在t值，使△PMQ是以PQ为直角边的等腰三角形？若存在请求出t值及点M的坐标；若不存在，请说明理由．

一个舞台要铺地毯（如图中的阴影部分，扇形的圆心角为90°），若按每铺1m²地毯所需30元计算，共需多少元（损耗不计）？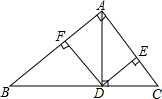

如图，在△ABC中，∠BAC=90°，AC≠AB，AD是斜边BC上的高，DE⊥AC，DF⊥AB，垂足分别为E、F，则图中与∠C（∠C除外）相等的角的个数是（　　）

如图，Rt△ABC中，AB=AC，BD平分∠ABC交AC于点D，过点C作CE⊥BD，交BD的延长线于点E，连接AE．若AE=1，则BE的长为

．

二次函数y=ax²+bx+c（a≠0）的图象如图所示，分析图象可知：
当k

时，方程ax²+bx+c=k有两个相等实数根；
当k

时，方程ax²+bx+c=k有两个不相等的实数根；
当k

试题分类