题目内容
 如图,点E是矩形ABCD中CD边上一点,△BCE沿BE折叠为△BFE,点F落在AD上,AB=3,BC=5,tan∠AFB=
如图,点E是矩形ABCD中CD边上一点,△BCE沿BE折叠为△BFE,点F落在AD上,AB=3,BC=5,tan∠AFB=考点:翻折变换(折叠问题)
专题:
分析:由折叠变换的性质得BF=BC=5;由勾股定理求出AF的长,即可解决问题.
解答: 解:如图,∵四边形ABCD为矩形,
解:如图,∵四边形ABCD为矩形,
∴∠A=90°;
由折叠变换的性质得:BF=BC=5;
由勾股定理得:
AF2=BF2-AB2,而AB=3,
∴AF=4,tan∠AFB=
=
.
故答案为
.
 解:如图,∵四边形ABCD为矩形,
解:如图,∵四边形ABCD为矩形,∴∠A=90°;
由折叠变换的性质得:BF=BC=5;
由勾股定理得:
AF2=BF2-AB2,而AB=3,
∴AF=4,tan∠AFB=
| AB |
| AF |
| 3 |
| 4 |
故答案为
| 3 |
| 4 |
点评:该题主要考查了翻折变换及其应用问题;牢固掌握、灵活运用有关定理是解题的关键.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
如果把
的x与y都扩大10倍,那么这个代数式的值( )
| 2x |
| x-y |
| A、不变 | ||
| B、扩大20倍 | ||
| C、扩大10倍 | ||
D、缩小到原来的
|
 如图,
如图,
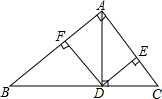 如图,在△ABC中,∠BAC=90°,AC≠AB,AD是斜边BC上的高,DE⊥AC,DF⊥AB,垂足分别为E、F,则图中与∠C(∠C除外)相等的角的个数是( )
如图,在△ABC中,∠BAC=90°,AC≠AB,AD是斜边BC上的高,DE⊥AC,DF⊥AB,垂足分别为E、F,则图中与∠C(∠C除外)相等的角的个数是( )