题目内容
2014年8月16日至28日,第二届夏季青年奥林匹克运动会在南京成功举办,某商场在这期间出售了一批进价为2元的“青年奥林匹克运动会”纪念卡,在市场营销中发现,此商品的日销售单价x(单位:元)与日销售数量y(单位:张)之间有如下关系
(1)根据表中数据在平面直角坐标系中描出实数对(x,y)的对应点;
(2)确定y与x之间的函数关系式,并画出图象;
(3)设销售此纪念卡的日纯利润为W元,试求出W与x之间的函数关系式,若物价局规定该纪念卡售价最高不超过10元/张,请你求出日销售单价x定位多少元时,才能获得最大日销售利润?
| 销售单价x(元) | 3 | 4 | 5 | 6 |
| 日销售量y(元) | 20 | 15 | 12 | 10 |
(2)确定y与x之间的函数关系式,并画出图象;
(3)设销售此纪念卡的日纯利润为W元,试求出W与x之间的函数关系式,若物价局规定该纪念卡售价最高不超过10元/张,请你求出日销售单价x定位多少元时,才能获得最大日销售利润?
考点:二次函数的应用
专题:
分析:(1)画出平面直角坐标系,运用描点法描出相应的点即可;
(2)设y与x之间的函数关系式为y=
,由待定系数法求出其解,再用描点法画出图象即可;
(3)根据利润=(售价-进价)×数量就可以求出解析式,再由二次函数的性质就可以求出结论.
(2)设y与x之间的函数关系式为y=
| k |
| x |
(3)根据利润=(售价-进价)×数量就可以求出解析式,再由二次函数的性质就可以求出结论.
解答:解:(1)由题意,得

(2)设y与x之间的函数关系式为y=
,由题意,得
20=
,
∴k=60.
y=
.
列表为:
描点并连线为:

(3)由题意,得
w=(x-2)y,
w=(x-2)×
,
w=60-
.
∵x≤10,
∴当x=10时,
w最大=48元.
答:日销售单价x定位10元时,才能获得最大日销售利润48元.

(2)设y与x之间的函数关系式为y=
| k |
| x |
20=
| k |
| 3 |
∴k=60.
y=
| 60 |
| x |
列表为:
| x | 3 | 4 | 5 | 6 | ||
y=
| 20 | 15 | 12 | 10 |

(3)由题意,得
w=(x-2)y,
w=(x-2)×
| 60 |
| x |
w=60-
| 120 |
| x |
∵x≤10,
∴当x=10时,
w最大=48元.
答:日销售单价x定位10元时,才能获得最大日销售利润48元.
点评:本题考查了运用待定系数法求函数的解析式的运用,描点法画函数图象的运用,反比例函数的性质的运用,解答时求出函数的解析式是关键.

练习册系列答案
 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
| 72+242 |
A、
| ||
B、±
| ||
| C、5 | ||
| D、±5 |
室外温度为-2℃,室内温度为3℃,则室内比室外的温度高( )
| A、1℃ | B、-1℃ |
| C、5℃ | D、-5℃ |
 如图,
如图,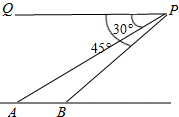 青海玉树地震后,抢险队派一架直升机去A,B两个村庄抢险,直升机在上空500m的P处测得A村的俯角为30°,B村的俯角为45°,如图,求A,B两个村庄之间的距离.(结果精确到1m)
青海玉树地震后,抢险队派一架直升机去A,B两个村庄抢险,直升机在上空500m的P处测得A村的俯角为30°,B村的俯角为45°,如图,求A,B两个村庄之间的距离.(结果精确到1m)
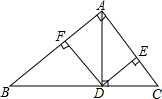 如图,在△ABC中,∠BAC=90°,AC≠AB,AD是斜边BC上的高,DE⊥AC,DF⊥AB,垂足分别为E、F,则图中与∠C(∠C除外)相等的角的个数是( )
如图,在△ABC中,∠BAC=90°,AC≠AB,AD是斜边BC上的高,DE⊥AC,DF⊥AB,垂足分别为E、F,则图中与∠C(∠C除外)相等的角的个数是( )