题目内容
18.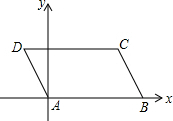 在?ABCD中,AB=5,AD=2,∠DAB=120°,若以点A为原点,直线AB为x轴,如图建立直角坐标系,则C的坐标是(4,$\sqrt{3}$).
在?ABCD中,AB=5,AD=2,∠DAB=120°,若以点A为原点,直线AB为x轴,如图建立直角坐标系,则C的坐标是(4,$\sqrt{3}$).
分析 过点D作DE⊥x轴于点E,在Rt△ADE中求出AE、DE,继而可得出点D的坐标,由平行四边形的性质可得点C的坐标.
解答 解:点B的坐标为(5,0),
过点D作DE⊥x轴于点E,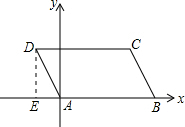
在Rt△ADE中,∠DAE=60°,AD=2,
∴AE=1,DE=$\sqrt{3}$,
故可得点D的坐标为(-1,$\sqrt{3}$),
又∵四边形ABCD是平行四边形,CD=AB=5,
∴点C的坐标为(4,$\sqrt{3}$),
故答案为:(4,$\sqrt{3}$).
点评 本题考查了平行四边形的性质及勾股定理的知识,属于基础题,熟知并掌握平行四边形的对边平行且相等是解题关键.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
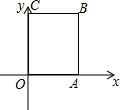 如图建立平面直角坐标系,长方形OABC中A(8,0),点C(0,10),点P从原点出发,以每秒1个单位长度的速度沿着O-C-B-A-O的路线运动到点O停止,设点P运动时间为t秒.
如图建立平面直角坐标系,长方形OABC中A(8,0),点C(0,10),点P从原点出发,以每秒1个单位长度的速度沿着O-C-B-A-O的路线运动到点O停止,设点P运动时间为t秒.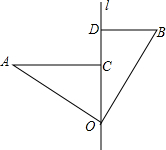 如图,点O是直线l上一点,点A、B位于直线l的两侧,且∠AOB=90°,OA=OB,分别过A、B两点作AC⊥l,交直线l于点C,BD⊥l,交直线l于点D.
如图,点O是直线l上一点,点A、B位于直线l的两侧,且∠AOB=90°,OA=OB,分别过A、B两点作AC⊥l,交直线l于点C,BD⊥l,交直线l于点D.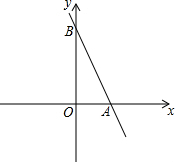 已知直线y=-2x+6与x轴交于点A,与y轴交于点B.
已知直线y=-2x+6与x轴交于点A,与y轴交于点B.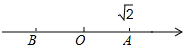 如图,数轴上点A表示$\sqrt{2}$,点A关于原点的对称点为B,设点B所表示的数字为x,求(x-$\sqrt{2}$)2+$\sqrt{2}$x的值.
如图,数轴上点A表示$\sqrt{2}$,点A关于原点的对称点为B,设点B所表示的数字为x,求(x-$\sqrt{2}$)2+$\sqrt{2}$x的值.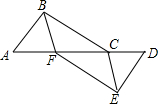 已知:如图,△FAB≌△CDE,BC=EF.求证:∠ACB=∠DFE.
已知:如图,△FAB≌△CDE,BC=EF.求证:∠ACB=∠DFE.