题目内容
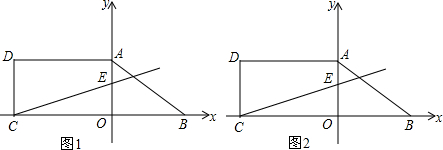
9. 二次函数y=ax2+bx+c的图象如图所示,则在下列说法中,与此函数的系数相关的一元二次方程ax2+bx+c=0的根的情况,说法正确的是( )
二次函数y=ax2+bx+c的图象如图所示,则在下列说法中,与此函数的系数相关的一元二次方程ax2+bx+c=0的根的情况,说法正确的是( )| A. | 方程有两个相等的实数根 | B. | 方程的实数根的积为负数 | ||
| C. | 方程有两个正的实数根 | D. | 方程没有实数根 |
分析 根据抛物线与x轴交点个数和位置判断一元二次方程ax2+bx+c=0的根的情况即可.
解答 解:根据图象可以看出抛物线与x轴有两个不同的交点,
故与此函数的系数相关的一元二次方程ax2+bx+c=0有两个不相等的实数根,
由于两交点位于原点的两侧,
故一元二次方程ax2+bx+c=0有一正根一负根,故只有B正确;
故选:B.
点评 本题考查了抛物线与x轴的交点.根据图象与x轴交点的个数和位置判断一元二次方程根的情况.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
4.某完全中学(含初、高中)篮球队12名队员的年龄情况如下:
(1)这个队队员年龄的众数是15,中位数是16;
(2)求这个队队员的平均年龄;
(3)若把这个队队员年龄绘成扇形统计图,请求出年龄为15岁对应的圆心角的度数.
| 年龄(单位:岁) | 14 | 15 | 16 | 17 | 18 |
| 人 数 | 1 | 4 | 3 | 2 | 2 |
(2)求这个队队员的平均年龄;
(3)若把这个队队员年龄绘成扇形统计图,请求出年龄为15岁对应的圆心角的度数.
18.对于二次函数y=3(x-1)2,下列结论正确的是( )
| A. | 当x取任何实数时,y的值总是正的 | B. | 其图象的顶点坐标为(0,1) | ||
| C. | 当x>1时,y随x的增大而增大 | D. | 其图象关于x轴对称 |
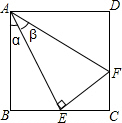 如图,E是正方形ABCD中BC边上的任意一点,连接AE,过点E作EF⊥AE交CD于点F,设∠BAE=α,∠EAF=β.求证:若E是BC的中点,则α=β,AF=AB+CF.
如图,E是正方形ABCD中BC边上的任意一点,连接AE,过点E作EF⊥AE交CD于点F,设∠BAE=α,∠EAF=β.求证:若E是BC的中点,则α=β,AF=AB+CF.