题目内容
18.若点(-1,4),(3,4)是抛物线y=ax2+bx+c上的两点,则此抛物线的对称轴是( )| A. | 直线x=-$\frac{b}{a}$ | B. | 直线x=1 | C. | 直线x=3 | D. | 直线x=2 |
分析 因为两点的纵坐标都为4,所以可判此两点是一对对称点,利用公式x=$\frac{{x}_{1}+{x}_{2}}{2}$求解即可.
解答 解:∵两点的纵坐标都为4,
∴此两点是一对对称点,
∴对称轴x=$\frac{{x}_{1}+{x}_{2}}{2}$=$\frac{-1+3}{2}$=1.
故选B.
点评 本题考查了如何求二次函数的对称轴,对于此类题目可以用公式法也可以将函数化为顶点式或用公式x=$\frac{{x}_{1}+{x}_{2}}{2}$求解.

练习册系列答案
 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
8.下列说法错误的是( )
| A. | 棱锥的侧面都是三角形 | B. | 棱柱的侧面不都是长方形 | ||
| C. | 正棱锥的所有侧棱都相等 | D. | 棱柱的所有棱都相等 |
8.-4的相反数是( )
| A. | 4 | B. | -4 | C. | -$\frac{1}{4}$ | D. | $\frac{1}{4}$ |
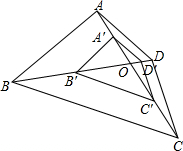 如图,四边形ABCD的对角线相交于点O,A′,B′,C′,D′分别是OA,0B,OC,OD的中点,试判断四边形ABCD与四边形A′B′C′D′是否相似,并说明理由.
如图,四边形ABCD的对角线相交于点O,A′,B′,C′,D′分别是OA,0B,OC,OD的中点,试判断四边形ABCD与四边形A′B′C′D′是否相似,并说明理由. 如图,O是直线AB上的一点,OC是△BOD的平分线,已知∠AOD=113°24′,求∠COD的度数.
如图,O是直线AB上的一点,OC是△BOD的平分线,已知∠AOD=113°24′,求∠COD的度数. 如图,已知△ABC和△DBE均为等边三角形,连接AD,CE,若∠BAD=36°,那么∠ACE=96°.
如图,已知△ABC和△DBE均为等边三角形,连接AD,CE,若∠BAD=36°,那么∠ACE=96°.