题目内容
7. 如图,已知△ABC和△DBE均为等边三角形,连接AD,CE,若∠BAD=36°,那么∠ACE=96°.
如图,已知△ABC和△DBE均为等边三角形,连接AD,CE,若∠BAD=36°,那么∠ACE=96°.
分析 根据SAS证明△ABD与△CBE全等,再利用全等三角形的性质解答即可.
解答 解:∵△ABC和△DBE均为等边三角形,
∴AB=BC,BD=BE,∠ABC=∠BBE=60°,
∴∠ABD=∠CBE,
在△ABC和△DBE中,
$\left\{\begin{array}{l}{AB=BC}\\{∠ABD=∠CBE}\\{BD=BE}\end{array}\right.$,
∴△ABD≌△CBE(SAS),
∴∠BCE=∠BAD=36°,
∴∠ACE=60°+36°=96°.
故答案为:96°.
点评 此题考查全等三角形的判定和性质,关键是根据SAS证明△ABD与△CBE全等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.下列各式中,大小比较错误的是( )
| A. | -(-$\frac{1}{3}$)>-$\frac{1}{3}$ | B. | -3$\frac{1}{5}$>-3.5 | C. | -(-3)<|-3| | D. | -1.1<0 |
18.若点(-1,4),(3,4)是抛物线y=ax2+bx+c上的两点,则此抛物线的对称轴是( )
| A. | 直线x=-$\frac{b}{a}$ | B. | 直线x=1 | C. | 直线x=3 | D. | 直线x=2 |
15.将y=x2向左平移3个单位长度,得( )
| A. | y=x2-3 | B. | y=x2+3 | C. | y=(x-3)2 | D. | y=(x+3)2 |

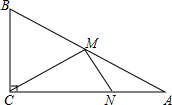 如图,在Rt△ABC中,AC=4,BC=3,若点M、N分别是线段AB、AC上的两个动点,则CM+MN的最小值为$\frac{96}{25}$.
如图,在Rt△ABC中,AC=4,BC=3,若点M、N分别是线段AB、AC上的两个动点,则CM+MN的最小值为$\frac{96}{25}$.