题目内容
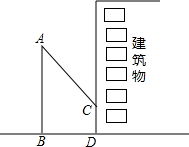 小明想利用校园内松树的树影测量树的高度,他在某一时刻测得长为1m的侧杆的影长为0.9m,但当他要测松树的影长时,因为树的影子恰好有一部分落在一座建筑物的墙上,如图所示,他先测得松树留在墙上的影子高CD=1.2m,又测得松树在地面上的影长BD=2.7m,请你帮助小明求出松树的高度.
小明想利用校园内松树的树影测量树的高度,他在某一时刻测得长为1m的侧杆的影长为0.9m,但当他要测松树的影长时,因为树的影子恰好有一部分落在一座建筑物的墙上,如图所示,他先测得松树留在墙上的影子高CD=1.2m,又测得松树在地面上的影长BD=2.7m,请你帮助小明求出松树的高度.考点:相似三角形的应用
专题:
分析:先求出墙上的影高CD落在地面上时的长度,再设树高为h,根据同一时刻物高与影长成正比列出关系式求出h的值即可.
解答:
解:设墙上的影高CD落在地面上时的长度为xm,树高为hm,
∵某一时刻测得长为1m的侧杆的影长为0.9m,墙上的影子高CD=1.2m,
∴
=
,解得x=1.08,
∴树的影长为:1.08+2.7=3.78(m),
∴
=
,
解得h=4.2.
答:松树的高度为4.2米.
∵某一时刻测得长为1m的侧杆的影长为0.9m,墙上的影子高CD=1.2m,
∴
| 1 |
| 0.9 |
| 1.2 |
| x |
∴树的影长为:1.08+2.7=3.78(m),
∴
| 1 |
| 0.9 |
| h |
| 3.78 |
解得h=4.2.
答:松树的高度为4.2米.
点评:本题考查的是相似三角形的应用,解答此题的关键是正确求出树的影长,这是此题的易错点.

练习册系列答案
相关题目
下列图案均是用长度相等的小木棒按一定规律拼搭而成的:拼搭图1需要4根小木棒,拼搭图2需13跟小木棒,拼搭图3需26根小木棒,照此规律,拼搭图6需小木棒的根数是( )


| A、64 | B、78 | C、89 | D、118 |
下列各组数据,可以构成三角形的是( )
| A、1、2、1 |
| B、2、2、1 |
| C、1、3、1 |
| D、2、2、5 |

 为迎接中考,4月初,学校体育组对901班50名学生进行了跳绳项目的测试,根据测试结果,列出部分频数分布表和绘制出部分频数分布直方图如图所示.
为迎接中考,4月初,学校体育组对901班50名学生进行了跳绳项目的测试,根据测试结果,列出部分频数分布表和绘制出部分频数分布直方图如图所示.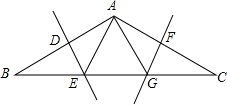 如图,在△ABC中,AB=AC,∠BAC=120°,DE,FG分别是AB,AC的垂直平分线,且BC=12,则EG=
如图,在△ABC中,AB=AC,∠BAC=120°,DE,FG分别是AB,AC的垂直平分线,且BC=12,则EG= 已知长方形ABCO,O为坐标原点,B的坐标为(6,5),A、C分别在坐标轴上,P是线段BC上的动点,设PC=m,已知D在第一象限且是直线y=2x-4上的一点,若△APD是等腰直角三角形,则点D的坐标为
已知长方形ABCO,O为坐标原点,B的坐标为(6,5),A、C分别在坐标轴上,P是线段BC上的动点,设PC=m,已知D在第一象限且是直线y=2x-4上的一点,若△APD是等腰直角三角形,则点D的坐标为