题目内容
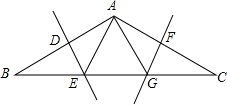 如图,在△ABC中,AB=AC,∠BAC=120°,DE,FG分别是AB,AC的垂直平分线,且BC=12,则EG=
如图,在△ABC中,AB=AC,∠BAC=120°,DE,FG分别是AB,AC的垂直平分线,且BC=12,则EG=考点:线段垂直平分线的性质
专题:
分析:先根据等腰三角形的性质求出∠B的度数,再由线段垂直平分线的性质得出∠BAE及∠CAG的度数,故可得出∠EAG的度数,判断出△AEG的形状,进而可得出结论.
解答:
解:∵在△ABC中,AB=AC,∠BAC=120°,
∴∠B=∠C=
=30°.
∵DE,FG分别是AB,AC的垂直平分线,
∴AE=BE,AG=CG,
∴∠B=∠BAE=30°,∠C=∠CAG=30°,
∴∠EAG=120°-30°-30°=60°.
∵∠AEG是△ABE的外角,
∴∠AEG=∠B+∠BAE=30°+30°=60°,
∴△AEG是等边三角形,
∴EG=
=
=4.
故答案为:4.
∴∠B=∠C=
| 180°-120° |
| 2 |
∵DE,FG分别是AB,AC的垂直平分线,
∴AE=BE,AG=CG,
∴∠B=∠BAE=30°,∠C=∠CAG=30°,
∴∠EAG=120°-30°-30°=60°.
∵∠AEG是△ABE的外角,
∴∠AEG=∠B+∠BAE=30°+30°=60°,
∴△AEG是等边三角形,
∴EG=
| BC |
| 3 |
| 12 |
| 3 |
故答案为:4.
点评:本题考查的是线段垂直平分线的性质,熟知线段垂直平分线上任意一点,到线段两端点的距离相等是解答此题的关键.

练习册系列答案
相关题目
下列各式正确的是( )
A、
| ||
B、
| ||
C、
| ||
D、-
|
有理数2.5,-8,
,-
,0,0.7,1中整数的个数有( )
| 3 |
| 2 |
| 2 |
| 7 |
| A、1 | B、2 | C、3 | D、4 |
 如图,AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,且DB=DC,求证:
如图,AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,且DB=DC,求证: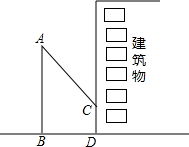 小明想利用校园内松树的树影测量树的高度,他在某一时刻测得长为1m的侧杆的影长为0.9m,但当他要测松树的影长时,因为树的影子恰好有一部分落在一座建筑物的墙上,如图所示,他先测得松树留在墙上的影子高CD=1.2m,又测得松树在地面上的影长BD=2.7m,请你帮助小明求出松树的高度.
小明想利用校园内松树的树影测量树的高度,他在某一时刻测得长为1m的侧杆的影长为0.9m,但当他要测松树的影长时,因为树的影子恰好有一部分落在一座建筑物的墙上,如图所示,他先测得松树留在墙上的影子高CD=1.2m,又测得松树在地面上的影长BD=2.7m,请你帮助小明求出松树的高度. 如图,直线l的函数关系式为y=kx+b-1,则3b与2k的大小关系是?
如图,直线l的函数关系式为y=kx+b-1,则3b与2k的大小关系是?