题目内容
用黑白两种颜色的正方形纸片,按黑色纸片数逐渐加1的规律拼成一系列图案,请仔细观察,并回答下列问题:

(1)第4个图案中有黑色纸片 张,有白色纸片 张;
(2)求第n个图案中有白色纸片多少张(用含n的代数式表示);
(3)求第几个图案有白色纸片2014张.

(1)第4个图案中有黑色纸片
(2)求第n个图案中有白色纸片多少张(用含n的代数式表示);
(3)求第几个图案有白色纸片2014张.
考点:规律型:图形的变化类
专题:
分析:(1)(2)依据图形找出其中的规律,即第n个图案中共有白纸片5n-(2n-1)=3n+1张,代入求解即可;
(3)由(2)中的结论代入求解即可.
(3)由(2)中的结论代入求解即可.
解答:
解:(1)第4个图案中有黑色纸片4张,有白色纸片13张;
(2)第一个图案中共有白纸片4张,即5×1-1;
第二个图案中共有白纸片7张,即5×2-3;
第三个图案中共有白纸片10张,即5×3-5;
…
第n个图案中共有白纸片5n-(2n-1)=3n+1张.
(2)3n+1=2014,解得n=671,
即第671个图案中共有白纸片2014张.
(2)第一个图案中共有白纸片4张,即5×1-1;
第二个图案中共有白纸片7张,即5×2-3;
第三个图案中共有白纸片10张,即5×3-5;
…
第n个图案中共有白纸片5n-(2n-1)=3n+1张.
(2)3n+1=2014,解得n=671,
即第671个图案中共有白纸片2014张.
点评:本题主要考查了图形的变化规律,能够通过观察,掌握其内在规律,进而求解.

练习册系列答案
相关题目
要使二次根式
有意义,则x的取值范围是( )
| 2-x |
| A、x>0 | B、x≤2 |
| C、x≥2 | D、x≥-2 |
一个长方形的一边长为2a+3b,另一边长为a+b,则这个长方形的周长是( )
| A、12a+16b |
| B、6a+8b |
| C、3a+4b |
| D、2a2+5ab+3b2 |
 如图,AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,且DB=DC,求证:
如图,AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,且DB=DC,求证: 如图,AB、PA是⊙O内接正n边形的相邻两边,切线PM与BA的延长线相交于点M,∠PMB=112.5°,求边数n.
如图,AB、PA是⊙O内接正n边形的相邻两边,切线PM与BA的延长线相交于点M,∠PMB=112.5°,求边数n. 如图,已知EF∥AD,∠1=∠2,∠BAD=70°,求∠AGD(请填空)
如图,已知EF∥AD,∠1=∠2,∠BAD=70°,求∠AGD(请填空)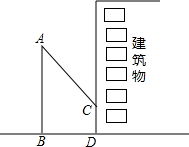 小明想利用校园内松树的树影测量树的高度,他在某一时刻测得长为1m的侧杆的影长为0.9m,但当他要测松树的影长时,因为树的影子恰好有一部分落在一座建筑物的墙上,如图所示,他先测得松树留在墙上的影子高CD=1.2m,又测得松树在地面上的影长BD=2.7m,请你帮助小明求出松树的高度.
小明想利用校园内松树的树影测量树的高度,他在某一时刻测得长为1m的侧杆的影长为0.9m,但当他要测松树的影长时,因为树的影子恰好有一部分落在一座建筑物的墙上,如图所示,他先测得松树留在墙上的影子高CD=1.2m,又测得松树在地面上的影长BD=2.7m,请你帮助小明求出松树的高度.