题目内容
下列图案均是用长度相等的小木棒按一定规律拼搭而成的:拼搭图1需要4根小木棒,拼搭图2需13跟小木棒,拼搭图3需26根小木棒,照此规律,拼搭图6需小木棒的根数是( )


| A、64 | B、78 | C、89 | D、118 |
考点:规律型:图形的变化类
专题:
分析:由题意可知,先算横着的小棒根数,再算竖着的小棒根数,进一步找出数字的规律,利用规律得出答案即可.
解答:
解:拼搭图1需要1×2+1+1=4根小木棒,
拼搭图2需(1+2)×2+1+3+3=13跟小木棒,
拼搭图3需(1+2+3)×2+1+3+5+5=26根小木棒,
…
拼搭图n需(1+2+3+…+n)×2+1+3+5+…+(2n-1)+(2n-1)=n(n+1)+n2+2n-1根小木棒,
因此拼搭图6需小木棒的根数是6×(6+1)+62+2×6-1=89.
故选:C.
拼搭图2需(1+2)×2+1+3+3=13跟小木棒,
拼搭图3需(1+2+3)×2+1+3+5+5=26根小木棒,
…
拼搭图n需(1+2+3+…+n)×2+1+3+5+…+(2n-1)+(2n-1)=n(n+1)+n2+2n-1根小木棒,
因此拼搭图6需小木棒的根数是6×(6+1)+62+2×6-1=89.
故选:C.
点评:本题考查了图形的变化类问题,解题的关键是仔细观察图形,从最简单的图形开始,找到规律,利用规律求解即可.

练习册系列答案
相关题目
下列各式正确的是( )
A、
| ||
B、
| ||
C、
| ||
D、-
|
 实数a在数轴上对应的点如图所示,则a,-a,1的大小关系正确的是( )
实数a在数轴上对应的点如图所示,则a,-a,1的大小关系正确的是( )| A、a<-a<1 |
| B、-a<a<1 |
| C、1<-a<a |
| D、a<1<-a |
下列式子正确的是( )
A、
| ||
B、±
| ||
C、
| ||
D、±
|
 如图,AB、PA是⊙O内接正n边形的相邻两边,切线PM与BA的延长线相交于点M,∠PMB=112.5°,求边数n.
如图,AB、PA是⊙O内接正n边形的相邻两边,切线PM与BA的延长线相交于点M,∠PMB=112.5°,求边数n. 如图,已知EF∥AD,∠1=∠2,∠BAD=70°,求∠AGD(请填空)
如图,已知EF∥AD,∠1=∠2,∠BAD=70°,求∠AGD(请填空) 如图,工作流水线上放置5个机器人,还放置一个工具箱,5个机器人取工具的次数相同,若AB=BC=CD=DE,将工具箱放在何处,才能使机器人取工具花时间最少?若有n个机器人,在工具箱应放在何处?
如图,工作流水线上放置5个机器人,还放置一个工具箱,5个机器人取工具的次数相同,若AB=BC=CD=DE,将工具箱放在何处,才能使机器人取工具花时间最少?若有n个机器人,在工具箱应放在何处?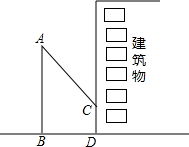 小明想利用校园内松树的树影测量树的高度,他在某一时刻测得长为1m的侧杆的影长为0.9m,但当他要测松树的影长时,因为树的影子恰好有一部分落在一座建筑物的墙上,如图所示,他先测得松树留在墙上的影子高CD=1.2m,又测得松树在地面上的影长BD=2.7m,请你帮助小明求出松树的高度.
小明想利用校园内松树的树影测量树的高度,他在某一时刻测得长为1m的侧杆的影长为0.9m,但当他要测松树的影长时,因为树的影子恰好有一部分落在一座建筑物的墙上,如图所示,他先测得松树留在墙上的影子高CD=1.2m,又测得松树在地面上的影长BD=2.7m,请你帮助小明求出松树的高度.