题目内容
 已知长方形ABCO,O为坐标原点,B的坐标为(6,5),A、C分别在坐标轴上,P是线段BC上的动点,设PC=m,已知D在第一象限且是直线y=2x-4上的一点,若△APD是等腰直角三角形,则点D的坐标为
已知长方形ABCO,O为坐标原点,B的坐标为(6,5),A、C分别在坐标轴上,P是线段BC上的动点,设PC=m,已知D在第一象限且是直线y=2x-4上的一点,若△APD是等腰直角三角形,则点D的坐标为考点:一次函数图象上点的坐标特征,等腰直角三角形
专题:分类讨论
分析:当点D位于直线y=2x-4上时,分三种情况考虑:如图②所示,当∠ADP=90°时,AD=PD,设D点坐标为(x,2x-4),利用三角形全等得到6-x=3,得x=3,易得D点坐标;如图3所示,当∠APD=90°时,AP=PD,设点P的坐标为(6,m),表示出D点坐标为(12-m,m+6),列出关于m的方程,求出m的值,即可确定出D点坐标;如图4所示,当∠ADP=90°时,AD=PD时,同理求出D的坐标,综上,得到所有满足题意D得坐标.
解答:
解:存在点D,使△APD是等腰直角三角形,理由为:
如图2所示,
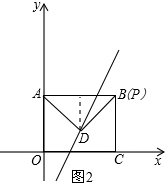
当∠ADP=90°时,AD=PD,易得D点坐标(3,2);
如图3所示,
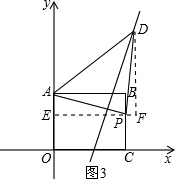
当∠APD=90°时,AP=PD,设点P的坐标为(6,m),
则D点坐标为(12-m,m+6),由m+6=2(12-m)-4,得m=
,
∴D点坐标(
,
);
如图4所示,当∠ADP=90°时,AD=PD时,
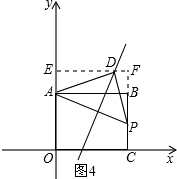
同理可求得D点坐标(
,
),
综上,符合条件的点D存在,坐标分别为(3,2),(
,
),(
,
).
故答案为:(3,2),(
,
),(
,
).
如图2所示,

当∠ADP=90°时,AD=PD,易得D点坐标(3,2);
如图3所示,

当∠APD=90°时,AP=PD,设点P的坐标为(6,m),
则D点坐标为(12-m,m+6),由m+6=2(12-m)-4,得m=
| 14 |
| 3 |
∴D点坐标(
| 22 |
| 3 |
| 40 |
| 3 |
如图4所示,当∠ADP=90°时,AD=PD时,

同理可求得D点坐标(
| 16 |
| 3 |
| 20 |
| 3 |
综上,符合条件的点D存在,坐标分别为(3,2),(
| 22 |
| 3 |
| 40 |
| 3 |
| 16 |
| 3 |
| 20 |
| 3 |
故答案为:(3,2),(
| 22 |
| 3 |
| 40 |
| 3 |
| 16 |
| 3 |
| 20 |
| 3 |
点评:此题考查了一次函数综合题,涉及的知识有:全等三角形的判定与性质,等腰直角三角形的性质,利用了分类讨论及数形结合的思想,本题第二问注意考虑问题要全面,做到不重不漏.

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
 实数a在数轴上对应的点如图所示,则a,-a,1的大小关系正确的是( )
实数a在数轴上对应的点如图所示,则a,-a,1的大小关系正确的是( )| A、a<-a<1 |
| B、-a<a<1 |
| C、1<-a<a |
| D、a<1<-a |
 如图,从A村出发到D村,最近的路线是( )
如图,从A村出发到D村,最近的路线是( )| A、A-B-C-D |
| B、A-B-F-D |
| C、A-B-E-F-D |
| D、A-B-M-D |
下列式子正确的是( )
A、
| ||
B、±
| ||
C、
| ||
D、±
|
 如图,AB、PA是⊙O内接正n边形的相邻两边,切线PM与BA的延长线相交于点M,∠PMB=112.5°,求边数n.
如图,AB、PA是⊙O内接正n边形的相邻两边,切线PM与BA的延长线相交于点M,∠PMB=112.5°,求边数n.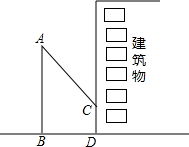 小明想利用校园内松树的树影测量树的高度,他在某一时刻测得长为1m的侧杆的影长为0.9m,但当他要测松树的影长时,因为树的影子恰好有一部分落在一座建筑物的墙上,如图所示,他先测得松树留在墙上的影子高CD=1.2m,又测得松树在地面上的影长BD=2.7m,请你帮助小明求出松树的高度.
小明想利用校园内松树的树影测量树的高度,他在某一时刻测得长为1m的侧杆的影长为0.9m,但当他要测松树的影长时,因为树的影子恰好有一部分落在一座建筑物的墙上,如图所示,他先测得松树留在墙上的影子高CD=1.2m,又测得松树在地面上的影长BD=2.7m,请你帮助小明求出松树的高度.