题目内容
2.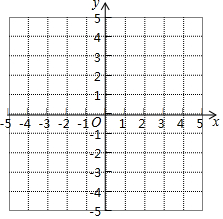 问题探索:在坐标平面内描出点A(2,0),B(4,0),C(-1,0),D(-3,0).
问题探索:在坐标平面内描出点A(2,0),B(4,0),C(-1,0),D(-3,0).(1)分别求出线段AB中点,线段AC中点及线段CD中点的坐标,则线段AB中点的坐标与点A,B的坐标之间有什么关系?对线段AC中点和点A,C及线段CD中点和点C,D成立吗?
(2)已知点M(a,0),N(b,0),请写出线段MN的中点P的坐标($\frac{a+b}{2}$,0).
结论猜想:
(3)若M(x1,y1),N(x2,y2),则MN的中点P的坐标为($\frac{{x}_{1}+{x}_{2}}{2}$,$\frac{{y}_{1}+{y}_{2}}{2}$).
拓展应用:
(4)若在平面直角坐标系中的点M,点N的坐标分别为M(2,y),N(x,-2),且P为MN的中点,若将线段MN向右平移3个单位后,与点P对应的点为Q,则点Q的坐标为(6,4),则x=4,y=10.
分析 (1)线段AB中点的横纵坐标分别为点A,B的横纵坐标的和的一半;整个结论对线段AC中点和点A,C及线段CD中点和点C,D成立
(2)、(3)利用(1)的结论易得线段MN的中点P的坐标;
(4)先利用点平移的坐标特征得到线段MN向右平移3个单位后,点M、N的对应点的坐标为(5,y),(x+3,-2),再利用线段中点坐标公式得到$\frac{5+x+3}{2}$=6,$\frac{y-2}{2}$=4,然后解方程即可求出x和y.
解答 解:(1)如图所示,
由坐标系可知,线段AB中点坐标为(3,0),线段AC中点坐标为(0.5,0),线段CD中点的坐标为(-2,0),
∵线段AB中点的横坐标3=$\frac{2+4}{2}$,纵坐标为0=$\frac{0+0}{2}$,
∴线段AB中点的坐标是点A,B的坐标的和的一半;
∵线段AC的中点的横坐标为0.5=$\frac{-1+2}{2}$,纵坐标0=$\frac{0+0}{2}$,
∴线段AC中点的横纵坐标分别是点A,C横纵坐标的和的一半;
∵线段CD的中点的横坐标为-2=$\frac{-1+(-3)}{2}$,纵坐标0=$\frac{0+0}{2}$,
∴线段CD中点的横纵坐标分别是点C、D横纵坐标的和的一半;
(2)由(1)知,线段MN的中点P的坐标为($\frac{a+b}{2}$,0),
故答案为:($\frac{a+b}{2}$,0);
(3)由(1)中规律知,MN的中点P的坐标为 ($\frac{{x}_{1}+{x}_{2}}{2}$,$\frac{{y}_{1}+{y}_{2}}{2}$),
故答案为:($\frac{{x}_{1}+{x}_{2}}{2}$,$\frac{{y}_{1}+{y}_{2}}{2}$);
(4)将线段MN向右平移3个单位后,点M、N的对应点的坐标为(5,y),(x+3,-2),而它们的中点坐标为(6,4),
所以$\frac{5+x+3}{2}$=6,$\frac{y-2}{2}$=4,
解得x=4,y=10.
故答案为,4,10.
点评 本题考查了作图-平移变换及线段的中点坐标公式,作图时要先找到图形的关键点,分别把这几个关键点按照平移的方向和距离确定对应点后,再顺次连接对应点即可得到平移后的图形,解题时得出各线段中点坐标规律是解题关键.

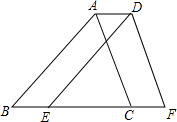 如图,将三角形ABC沿BC方向平移到三角形DEF,若AD=1,CE=3,则梯形ABFD的面积与三角形ABC的面积比是( )
如图,将三角形ABC沿BC方向平移到三角形DEF,若AD=1,CE=3,则梯形ABFD的面积与三角形ABC的面积比是( )| A. | 2:1 | B. | 3:2 | C. | 4:3 | D. | 不能确定 |
| A. | x(x-1)=21 | B. | x(x+1)=21 | C. | x(x-1)=42 | D. | x(x+1)=42 |
| 摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
| 摸到白球的次数m | 65 | 124 | 178 | 302 | 481 | 599 | 1803 |
| 摸到白球的频率$\frac{m}{n}$ | 0.65 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
| A. | -2 | B. | 2 | C. | -1 | D. | 1 |
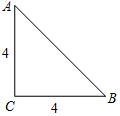 在数学活动课中,同学们准备了一些等腰直角三角形纸片,从每张纸片中剪出一个扇形制作圆锥玩具模型.如图,已知△ABC是腰长为4的等腰直角三角形.
在数学活动课中,同学们准备了一些等腰直角三角形纸片,从每张纸片中剪出一个扇形制作圆锥玩具模型.如图,已知△ABC是腰长为4的等腰直角三角形.