题目内容
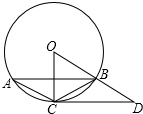 已知:如图,△ABC内接于⊙O,点D在半径OB延长线上,∠BCD=∠A=30°.
已知:如图,△ABC内接于⊙O,点D在半径OB延长线上,∠BCD=∠A=30°.(1)试判断直线CD与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为8,求BD的长.
考点:切线的判定
专题:
分析:(1)根据圆周角定理和等边三角形的判定证得△OBC是等边三角形,则∠OCB=60°,所以由图中相关角与角间的和差关系易求∠OCD=90°,即直线CD与⊙O相切;
(2)在直角△OCD中,利用“30度角所对的直角边等于斜边的一半”得到OD=2OC=16,则BD=OD-OB=16-8=8.
(2)在直角△OCD中,利用“30度角所对的直角边等于斜边的一半”得到OD=2OC=16,则BD=OD-OB=16-8=8.
解答: 解:(1)CD与⊙O相切,理由如下:
解:(1)CD与⊙O相切,理由如下:
∵∠A=30°
∴∠BOC=2∠A=60°.
又∵OB=OC,
∴△OBC是等边三角形,
∴∠OCB=60°,
∴∠OCD=∠OCB+∠BCD=60°+30°=90°,即OC⊥CD.
又OC是半径,
∴CD与⊙O相切;
(2)∵∠BOC=60°,∠OCD=90°,
∴∠D=30°,
∴OD=2OC=16,
∴BD=OD-OB=16-8=8.
 解:(1)CD与⊙O相切,理由如下:
解:(1)CD与⊙O相切,理由如下:∵∠A=30°
∴∠BOC=2∠A=60°.
又∵OB=OC,
∴△OBC是等边三角形,
∴∠OCB=60°,
∴∠OCD=∠OCB+∠BCD=60°+30°=90°,即OC⊥CD.
又OC是半径,
∴CD与⊙O相切;
(2)∵∠BOC=60°,∠OCD=90°,
∴∠D=30°,
∴OD=2OC=16,
∴BD=OD-OB=16-8=8.
点评:本题考查了切线的判定.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

练习册系列答案
相关题目
下列各数组中,能作为直角三角形三边长的是( )
| A、1,1,2 |
| B、2,3,4 |
| C、2,3,5 |
| D、3,4,5 |
如果a2+8ab+m是一个完全平方式,则m可以是( )
| A、b2 |
| B、2b |
| C、4b |
| D、16b2 |
下列方程无实数根的是( )
| A、x2=0 |
| B、x2-1=0 |
| C、x2+1=0 |
| D、x2-x=0 |
 已知直线y=
已知直线y=