题目内容
如果a2+8ab+m是一个完全平方式，则m可以是（ ）
| A、b2 |
| B、2b |
| C、4b |
| D、16b2 |
考点：完全平方式
专题：
分析：先根据已知平方项和乘积二倍项确定出这两个数，再根据完全平方公式即可确定m的值．
解答：解：∵a2+8ab+m=a2+2×a×4b+m，
∴m=（4b）2=16b2．
故选D．
∴m=（4b）2=16b2．
故选D．
点评：本题主要考查了完全平方式，根据已知平方项和乘积二倍项确定出这两个数是解题的关键，也是难点，熟记完全平方公式对解题非常重要．
练习册系列答案
相关题目
如图，在锐角△ABC中，AC=7cm，S△ABC=14cm2，AD平分∠BAC，M、N分别是AD和AB上的动点，则BM+MN的最小值是将4x2+1加上一个单项式所得的和为完全平方式，则这个单项式不可能是（ ）
| A、-4x4 |
| B、-4x |
| C、4x |
| D、4x4 |
如图图形中，既是轴对称图形，又是中心对称图形的是（ ）
A、 |
B、 |
C、 |
D、 |
下列4个命题的逆命题中真命题个数是（ ）
①同旁内角互补，两直线平行
②如果两个实数相等，那么这两个实数的平方相等
③线段垂直平分线上的点到线段两端的距离相等
④直角三角形的两条直角边的平方和等于斜边的平方．
①同旁内角互补，两直线平行
②如果两个实数相等，那么这两个实数的平方相等
③线段垂直平分线上的点到线段两端的距离相等
④直角三角形的两条直角边的平方和等于斜边的平方．
| A、1 | B、2 | C、3 | D、4 |
若
是方程ax-y=3的解，则a的值（ ）
|
| A、1 | B、2 | C、4 | D、-5 |
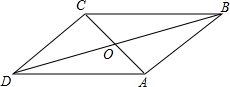如图，平行四边形ABCD中，对角线AC与BD交于点O，已知∠OAB=90°，BD=10cm，AC=6cm，则AB的长为（ ）| A、4cm | B、5cm |
| C、6cm | D、8cm |
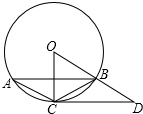已知：如图，△ABC内接于⊙O，点D在半径OB延长线上，∠BCD=∠A=30°．