题目内容
16.计算:($\frac{1}{\sqrt{2}+1}$+$\frac{1}{\sqrt{3}+\sqrt{2}}$+$\frac{1}{\sqrt{4}+\sqrt{3}}$+…+$\frac{1}{\sqrt{2017}+\sqrt{2016}}$)($\sqrt{2017}$+1).分析 先分母有理化,然后把括号内合并后利用平方差公式计算.
解答 解:原式=($\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+$\sqrt{4}$-$\sqrt{3}$+…+$\sqrt{2017}$-$\sqrt{2016}$)($\sqrt{2017}$+1)
=($\sqrt{2017}$-1)($\sqrt{2017}$+1)
=2017-1
=2016.
点评 本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
11.已知:|x|=1,|y|=$\frac{1}{2}$,则(x20)3-x3y2的值等于( )
| A. | $-\frac{3}{4}$或$-\frac{5}{4}$ | B. | $\frac{3}{4}$或$\frac{5}{4}$ | C. | $\frac{3}{4}$ | D. | -$\frac{5}{4}$ |
19.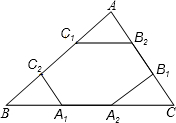 如图,点A1、A2、B1、B2、C1、C2分别为△ABC的边BC、CA、AB的三等分点,若△ABC的周长为I,则六边形A1A2B1B2C1C2的周长为( )
如图,点A1、A2、B1、B2、C1、C2分别为△ABC的边BC、CA、AB的三等分点,若△ABC的周长为I,则六边形A1A2B1B2C1C2的周长为( )
 如图,点A1、A2、B1、B2、C1、C2分别为△ABC的边BC、CA、AB的三等分点,若△ABC的周长为I,则六边形A1A2B1B2C1C2的周长为( )
如图,点A1、A2、B1、B2、C1、C2分别为△ABC的边BC、CA、AB的三等分点,若△ABC的周长为I,则六边形A1A2B1B2C1C2的周长为( )| A. | 2I | B. | $\frac{2}{3}$I | C. | $\frac{\sqrt{3}}{3}$I | D. | $\frac{1}{3}$I |
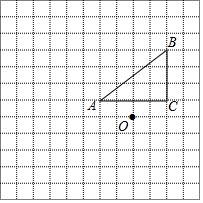 如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A、B、C都在格点上,将△ABC绕点A顺时针旋转90°,得到△AB′C′
如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A、B、C都在格点上,将△ABC绕点A顺时针旋转90°,得到△AB′C′ 如图,点D、E、F分别为△ABC的三边中点,试说明△ABC∽△EFD.
如图,点D、E、F分别为△ABC的三边中点,试说明△ABC∽△EFD.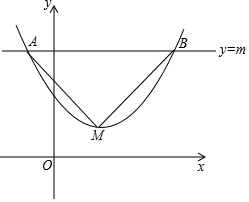 抛物线y=a(x-2)2+3(a>0),直线y=m交抛物线于A、B两点,M为顶点,△ABM为直角三角形,求AB的长.
抛物线y=a(x-2)2+3(a>0),直线y=m交抛物线于A、B两点,M为顶点,△ABM为直角三角形,求AB的长.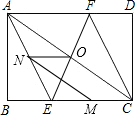 矩形ABCD中,AE平分∠BAC交BC于点E,CF平分∠ACD交AD于点F,连接EF,点M为EC的中点,N点为AE上的一个动点,AB=6
矩形ABCD中,AE平分∠BAC交BC于点E,CF平分∠ACD交AD于点F,连接EF,点M为EC的中点,N点为AE上的一个动点,AB=6