题目内容
19.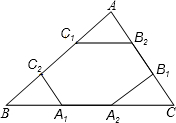 如图,点A1、A2、B1、B2、C1、C2分别为△ABC的边BC、CA、AB的三等分点,若△ABC的周长为I,则六边形A1A2B1B2C1C2的周长为( )
如图,点A1、A2、B1、B2、C1、C2分别为△ABC的边BC、CA、AB的三等分点,若△ABC的周长为I,则六边形A1A2B1B2C1C2的周长为( )| A. | 2I | B. | $\frac{2}{3}$I | C. | $\frac{\sqrt{3}}{3}$I | D. | $\frac{1}{3}$I |
分析 根据题意可知△ABC∽△AC1B2,△ABC∽△C2BA1,△ABC∽△B1A2C,推出C1B2:BC=1:3,C2A1:AC=1:3,B1A2:AB=1:3,推出六边形的周长为△ABC的周长L的$\frac{2}{3}$.
解答 解:∵点A1、A2,B1、B2,C1、C2分别是△ABC的边BC、CA、AB的三等分点,
∴△ABC∽△AC1B2,△ABC∽△C2BA1,△ABC∽△B1A2C,
∴C1B2:BC=1:3,C2A1:AC=1:3,B1A2:AB=1:3,
∴六边形A1A2B1B2C1C2的周长=$\frac{2}{3}$(AB+BC+CA),
∵△ABC的周长为I,
∴六边形A1A2B1B2C1C2的周长=$\frac{2}{3}$I.
故选:B.
点评 本题主要考查相似三角形的判定和性质、三角形周长、六边形周长,关键在于求证三角形相似.

练习册系列答案
相关题目
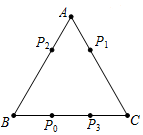 如图,电子跳蚤游戏盘是如图所示的△ABC,AB=BC=AC=6.如果跳蚤开始时在BC边的P0处,BP0=2.跳蚤第一步从P0跳到AC边的P1(第1次落点)处,且CP1=CP0;第二步从P1跳到AB边的P2(第2次落点)处,且AP2=AP1;第三步从P2跳到BC边的P3(第3次落点)处,且BP3=BP2…;跳蚤按照上述规则一直跳下去,第n次落点为Pn(n为正整数),则点P2012与点P2013之间的距离为( )
如图,电子跳蚤游戏盘是如图所示的△ABC,AB=BC=AC=6.如果跳蚤开始时在BC边的P0处,BP0=2.跳蚤第一步从P0跳到AC边的P1(第1次落点)处,且CP1=CP0;第二步从P1跳到AB边的P2(第2次落点)处,且AP2=AP1;第三步从P2跳到BC边的P3(第3次落点)处,且BP3=BP2…;跳蚤按照上述规则一直跳下去,第n次落点为Pn(n为正整数),则点P2012与点P2013之间的距离为( ) 如图,甲中的三个数存在某种关系,要让乙中的三个数也满足这种关系,那么乙中空白处的数应是( )
如图,甲中的三个数存在某种关系,要让乙中的三个数也满足这种关系,那么乙中空白处的数应是( ) 如图,△ABC,∠ACB=90°,点D,E分别在AB,BC上,AC=AD,∠CDE=45°,CD与
如图,△ABC,∠ACB=90°,点D,E分别在AB,BC上,AC=AD,∠CDE=45°,CD与 在△ABC中,∠ACB为直角,∠A=30°,CD⊥AB于D,若BD=1,则AB的长度是( )
在△ABC中,∠ACB为直角,∠A=30°,CD⊥AB于D,若BD=1,则AB的长度是( )