题目内容
2.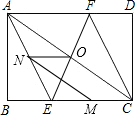 矩形ABCD中,AE平分∠BAC交BC于点E,CF平分∠ACD交AD于点F,连接EF,点M为EC的中点,N点为AE上的一个动点,AB=6
矩形ABCD中,AE平分∠BAC交BC于点E,CF平分∠ACD交AD于点F,连接EF,点M为EC的中点,N点为AE上的一个动点,AB=6(1)证明:△ABE≌△CDF;
(2)填空:①当BC=6$\sqrt{3}$时,四边形AECF为菱形;
②在①的条件下,当ON=2$\sqrt{3}$时,四边形ONMC为平行四边形.
分析 (1)只要证明∠BAE=∠FCD,即可根据ASA证明△ABE≌△CDF.
(2)当BC=6$\sqrt{3}$时,四边形AECF是菱形.通过计算求出AF=FC,再证明四边形AECF是平行四边形即可解决问题.
(3)当AN=NE时,先证明四边形ONMC是平行四边形,再求出ON的长即可.
解答 (1)证明:∵四边形ABCD是矩形,
∴AB=CD,AB∥CD,∠B=∠D=90°,
∴∠BAC=∠ACD,
∵∠BAE=$\frac{1}{2}$∠BAC,∠DCF=$\frac{1}{2}$∠ACD,
∴∠BAE=∠FCD,
在△ABE和△CDE中,
$\left\{\begin{array}{l}{∠BAE=∠DCF}\\{AB=CD}\\{∠B=∠D}\end{array}\right.$,
∴△ABE≌△CDF(ASA).
(2)当BC=6$\sqrt{3}$时,四边形AECF是菱形.
理由:在Rt△ADC中,∵AD=BC=6$\sqrt{3}$,DC=6,
∴tan∠DAC=$\frac{CD}{AD}$=$\frac{\sqrt{3}}{3}$,
∴∠DAC=30°,∠ACD=60°,
∴∠ACF=∠DCF=30°,
∴DF=CD•tan30°=2$\sqrt{3}$,
∴CF=2DF=4$\sqrt{3}$,AF=AD-DF=6$\sqrt{3}$-2$\sqrt{3}$=4$\sqrt{3}$,
∴AF=CF,
∵△ABE≌△CDF,
∴BE=DF,
∵AD=BC,
∴AF=CE,∵AF∥EC,
∴四边形AECF是平行四边形,
∵AF=FC,
∴四边形AECF是菱形.
故答案为6$\sqrt{3}$.
(3)当AN=NE时,∵四边形AECF是菱形,
∴OA=OC,
∴ON∥EC,
∵AN=NE,EM=CM,
∴NM∥AC,
∴四边形ONMC是平行四边形,
∴ON=CM=$\frac{1}{2}$EC=$\frac{1}{2}$×4$\sqrt{3}$=2$\sqrt{3}$.
故答案为2$\sqrt{3}$.
点评 本题考查四边形综合题、矩形的判定和性质、菱形的判定和性质、平行四边形的判定和性质等知识,锐角三角函数等知识,解题的关键是灵活运用所学知识解决问题,本题的突破点是利用特殊角30°解决问题,属于中考压轴题.

 名校课堂系列答案
名校课堂系列答案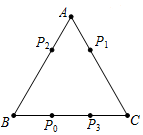 如图,电子跳蚤游戏盘是如图所示的△ABC,AB=BC=AC=6.如果跳蚤开始时在BC边的P0处,BP0=2.跳蚤第一步从P0跳到AC边的P1(第1次落点)处,且CP1=CP0;第二步从P1跳到AB边的P2(第2次落点)处,且AP2=AP1;第三步从P2跳到BC边的P3(第3次落点)处,且BP3=BP2…;跳蚤按照上述规则一直跳下去,第n次落点为Pn(n为正整数),则点P2012与点P2013之间的距离为( )
如图,电子跳蚤游戏盘是如图所示的△ABC,AB=BC=AC=6.如果跳蚤开始时在BC边的P0处,BP0=2.跳蚤第一步从P0跳到AC边的P1(第1次落点)处,且CP1=CP0;第二步从P1跳到AB边的P2(第2次落点)处,且AP2=AP1;第三步从P2跳到BC边的P3(第3次落点)处,且BP3=BP2…;跳蚤按照上述规则一直跳下去,第n次落点为Pn(n为正整数),则点P2012与点P2013之间的距离为( ) 如图,甲中的三个数存在某种关系,要让乙中的三个数也满足这种关系,那么乙中空白处的数应是( )
如图,甲中的三个数存在某种关系,要让乙中的三个数也满足这种关系,那么乙中空白处的数应是( ) 在△ABC中,∠ACB为直角,∠A=30°,CD⊥AB于D,若BD=1,则AB的长度是( )
在△ABC中,∠ACB为直角,∠A=30°,CD⊥AB于D,若BD=1,则AB的长度是( ) 已知一次函数y=kx+b的图象经过点A(-3,-2)及点B(-1,2).
已知一次函数y=kx+b的图象经过点A(-3,-2)及点B(-1,2).