题目内容
16．
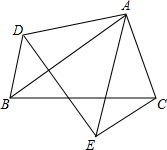如图，△ABC和△ADE中，∠BAC=∠DAE，AB=AE，AD=AC，连接BD，CE，若BD=8，求CE的长．
分析 利用SAS即可证得△ABC≌△AED，根据全等三角形的对应边相等即可求解．
解答 解：∵在△ABC和△AED中，
$\left\{\begin{array}{l}{AB=AE}\\{∠BAC=∠DAE}\\{AD=AC}\end{array}\right.$，
∴△ABC≌△AED，
∴CE=BD=8．
点评 本题考查了全等三角形的判定与性质，证明△ABC≌△AED是关键．
练习册系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
18．下列各式运算结果正确的是（ ）
| A． | 3x+3y=6xy | B． | -x+x=-2x | C． | 9y2-6y2=3 | D． | -9a2b-9a2b=0 |
11．
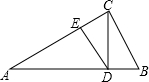如图，在Rt△ABC中，BC=a，AB=c，CD为斜边上的高，DE⊥AC．设△AED、△CDB、△ABC的周长分别为p1，p2，p，则当$\frac{{p}_{1}+{p}_{2}}{p}$取最大值时，sinA=（ ）
如图，在Rt△ABC中，BC=a，AB=c，CD为斜边上的高，DE⊥AC．设△AED、△CDB、△ABC的周长分别为p1，p2，p，则当$\frac{{p}_{1}+{p}_{2}}{p}$取最大值时，sinA=（ ）| A． | $\frac{1}{2}$ | B． | $\frac{2}{3}$ | C． | $\frac{\sqrt{2}}{2}$ | D． | $\frac{3}{4}$ |
如图，每个小正方形的边长为1．
如图，AD∥BC，∠BAD=90°．请按要求画图：以B为圆心，BC长为半径画弧，与射线AD交于点E，连结BE，过点C作CF⊥BE，垂足为F．线段BF与图中的哪一条线段相等？证明你的结论．