题目内容
1. 如图,每个小正方形的边长为1.
如图,每个小正方形的边长为1.(1)求四边形ABCD的面积;
(2)求∠BCD的度数.
分析 (1)根据四边形ABCD的面积=S矩形AEFH-S△AEB-S△BFC-S△CGD-S梯形AHGD即可得出结论;
(2)先根据锐角三角函数的定义判断出∠FBC=∠DCG,再根据直角三角形的性质可得出∠BCF+∠DCG=90°,故可得出结论.
解答 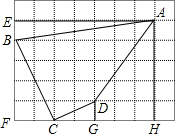 解:(1)∵四边形ABCD的面积
解:(1)∵四边形ABCD的面积
=S矩形AEFH-S△AEB-S△BFC-S△CGD-S梯形AHGD
=5×7-$\frac{1}{2}$×1×7-$\frac{1}{2}$×2×4-$\frac{1}{2}$×1×2-$\frac{1}{2}$(1+5)×3
=35-$\frac{7}{2}$-4-1-9
=17.5;
(2)∠BCD=90°;理由如下:
∵tan∠FBC=$\frac{2}{4}$=$\frac{1}{2}$,tan∠DCG=$\frac{1}{2}$,
∴∠FBC=∠DCG,
∵∠FBC+∠BCF=∠DCG+∠CDG=90°,
∴∠BCF+∠DCG=90°,
∴∠BCD=90°.
点评 本题考查的是勾股定理、三角函数以及三角形面积的计算,熟知勾股定理及直角三角形的性质是解答此题的关键.

练习册系列答案
相关题目
 如图,线段AB=16cm,点C是线段AB上一点.若点M是线段AC的中点,点N是线段BC的中点,则线段MN的长度为8cm.
如图,线段AB=16cm,点C是线段AB上一点.若点M是线段AC的中点,点N是线段BC的中点,则线段MN的长度为8cm. 已知:如图,在△ABC中,∠A=∠ABC,直线EF分别交△ABC的边AB、AC和CB的延长线于点D、E、F.求证:∠F+∠FEC=2∠A.
已知:如图,在△ABC中,∠A=∠ABC,直线EF分别交△ABC的边AB、AC和CB的延长线于点D、E、F.求证:∠F+∠FEC=2∠A.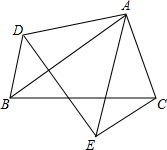 如图,△ABC和△ADE中,∠BAC=∠DAE,AB=AE,AD=AC,连接BD,CE,若BD=8,求CE的长.
如图,△ABC和△ADE中,∠BAC=∠DAE,AB=AE,AD=AC,连接BD,CE,若BD=8,求CE的长. 如图,在△ABC中,点D、E在BC上,且∠1=∠B,∠2=∠C,BC=10cm,求△ADE的周长.
如图,在△ABC中,点D、E在BC上,且∠1=∠B,∠2=∠C,BC=10cm,求△ADE的周长. 如图,在一张无穷大的格纸上,格点的位置可用数对(m,n)表示,如点A的位置为(3,3),点B的位置为(6,2).点M从(0,0)开始移动,规律为:第1次向右移动1个单位到(1,0),第2次向上移动2个单位到(1,2),第3次向右移动3个单位到(4,2),…,第n次移动n个单位(n为奇数时向右,n为偶数时向上),那么点M第27次移动到的位置为( )
如图,在一张无穷大的格纸上,格点的位置可用数对(m,n)表示,如点A的位置为(3,3),点B的位置为(6,2).点M从(0,0)开始移动,规律为:第1次向右移动1个单位到(1,0),第2次向上移动2个单位到(1,2),第3次向右移动3个单位到(4,2),…,第n次移动n个单位(n为奇数时向右,n为偶数时向上),那么点M第27次移动到的位置为( )