题目内容
6. 如图,AD∥BC,∠BAD=90°.请按要求画图:以B为圆心,BC长为半径画弧,与射线AD交于点E,连结BE,过点C作CF⊥BE,垂足为F.线段BF与图中的哪一条线段相等?证明你的结论.
如图,AD∥BC,∠BAD=90°.请按要求画图:以B为圆心,BC长为半径画弧,与射线AD交于点E,连结BE,过点C作CF⊥BE,垂足为F.线段BF与图中的哪一条线段相等?证明你的结论.
分析 先根据几何语言画出几何图形,再利用平行线的性质得到∠CBF=∠AEB,然后根据“AAS”可证明△ABE≌△FBC,从而得到BF=AE.
解答 解:如图,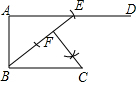
结论:BF=AE.
证明:∵AD∥BC,
∴∠CBF=∠AEB,
∵CF⊥BE,
∴∠BCF=90°,
在△ABE和△FBC中
$\left\{\begin{array}{l}{∠A=∠BFC}\\{∠AEB=∠CBF}\\{BE=BC}\end{array}\right.$,
∴△ABE≌△FBC(AAS),
∴BF=AE.
点评 本题考查了作图-基本作图:熟练掌握基本作图(作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线).也考查了全等三角形的判断与性质.

练习册系列答案
相关题目
17. 如图,矩形ABCD的外接圆O与水平地面有唯一交点A,圆O的半径为4,且$\widehat{BC}$=2$\widehat{AB}$.若在没有滑动的情况下,将圆O向右滚动,使得O点向右移动了98π,则此时该圆与地面交点在( )上.
如图,矩形ABCD的外接圆O与水平地面有唯一交点A,圆O的半径为4,且$\widehat{BC}$=2$\widehat{AB}$.若在没有滑动的情况下,将圆O向右滚动,使得O点向右移动了98π,则此时该圆与地面交点在( )上.
 如图,矩形ABCD的外接圆O与水平地面有唯一交点A,圆O的半径为4,且$\widehat{BC}$=2$\widehat{AB}$.若在没有滑动的情况下,将圆O向右滚动,使得O点向右移动了98π,则此时该圆与地面交点在( )上.
如图,矩形ABCD的外接圆O与水平地面有唯一交点A,圆O的半径为4,且$\widehat{BC}$=2$\widehat{AB}$.若在没有滑动的情况下,将圆O向右滚动,使得O点向右移动了98π,则此时该圆与地面交点在( )上.| A. | $\widehat{AB}$ | B. | $\widehat{BC}$ | C. | $\widehat{CD}$ | D. | $\widehat{DA}$ |
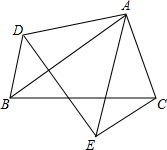 如图,△ABC和△ADE中,∠BAC=∠DAE,AB=AE,AD=AC,连接BD,CE,若BD=8,求CE的长.
如图,△ABC和△ADE中,∠BAC=∠DAE,AB=AE,AD=AC,连接BD,CE,若BD=8,求CE的长.
 如图所示,直线m是一次函数y=kx+b的图象.
如图所示,直线m是一次函数y=kx+b的图象. 如图,在一张无穷大的格纸上,格点的位置可用数对(m,n)表示,如点A的位置为(3,3),点B的位置为(6,2).点M从(0,0)开始移动,规律为:第1次向右移动1个单位到(1,0),第2次向上移动2个单位到(1,2),第3次向右移动3个单位到(4,2),…,第n次移动n个单位(n为奇数时向右,n为偶数时向上),那么点M第27次移动到的位置为( )
如图,在一张无穷大的格纸上,格点的位置可用数对(m,n)表示,如点A的位置为(3,3),点B的位置为(6,2).点M从(0,0)开始移动,规律为:第1次向右移动1个单位到(1,0),第2次向上移动2个单位到(1,2),第3次向右移动3个单位到(4,2),…,第n次移动n个单位(n为奇数时向右,n为偶数时向上),那么点M第27次移动到的位置为( )
 如图,在Rt△ABC中,点D在BC上,∠ADC=45°,DC=6,sinB=$\frac{3}{5}$,求∠BAD的正切值.
如图,在Rt△ABC中,点D在BC上,∠ADC=45°,DC=6,sinB=$\frac{3}{5}$,求∠BAD的正切值.